1 热膨胀-应力和力
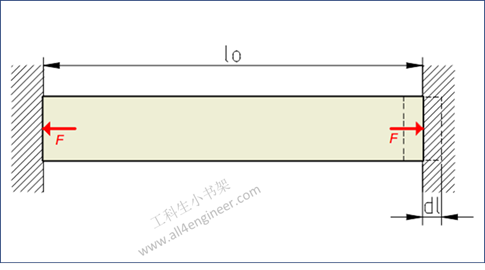
图 1
温度变化引起的线性膨胀可表示为:
dl = α l0 dt
式 1
其中:
- dl =伸长量(m)
- α= 温度膨胀系数(m / mK)某一方向上的长度的变化和它在20℃(即标准实验室环境)时的长度的比值
- l0=初始长度(m)
- dt =温差(°C)
若热膨胀无限制将产生的应变或变形可以表示为
ε= dl / l0
式 2
其中:
- ε=应变
由此产生的应力可以表示为:
σ = Eε
式 3
其中:
- E = 杨氏模量(Pa(N / m 2))
- σ= 应力(Pa(N / m 2),psi)
- ε=应变
因此两端被限制的圆柱所产生的轴向力可由下式计算:
F = σdt A
= E α dt A
式 4
其中:
- F = 轴向力 (N)
- A = 圆柱截面面积 (m2)
2 算例
图一中圆柱铸铁横截面面积为1000 mm2, 热膨胀系数为12.2×10-6 m/m·K,初始长度l0为300mm,杨氏模量为155GPa,温差为20 °C。
由此产生的轴向力可以计算为:
dl = (12.2×10-12 m/mK) (300 mm) (20 oC)
= 7.32×10-11 m
ε= dl / l0
=(7.32×10-11 m)/ (300mm)
=2.44×10-10
σ= Eε=(155 GPa) · 2.44×10-10=37.8 Pa (N/m2)
F= σdt A =(37.8 Pa)×(1000mm2) = 0.03782 N
