1 简支梁单点载荷计算
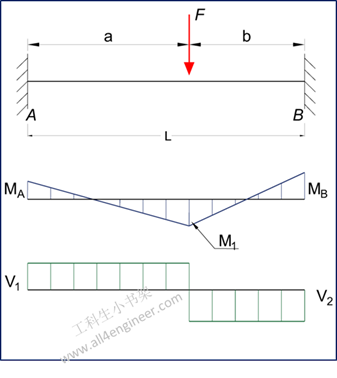
图 1
1.1 弯矩计算
MA = – F a b2 / L2
式 1
其中:
- MA =固定端A处的力矩(Nm)
- F = 载荷 (N)
MB = – F a2 b / L2
式 2
- MB =固定端B的力矩(Nm)
MF = 2 F a2 b2 / L3
式 3
- MF =点载荷时的力矩(Nm)
1.2 挠度计算
δF = F a3 b3 / (3 L3 E I)
式 4
- δF=点载荷时的挠度(m)
- E =弹性模量(Pa(N / m2),N / mm2)
- I =惯性面积矩(m4,mm4)
1.3 支反力计算
RA = F (3 a + b) b2 / L3
式 5
- RA =固定端A的支反力(N)
RB = F (a + 3 b) a2 / L3
式 6
- RB =固定端B的支反力(N)
2 简支梁的均布载荷计算
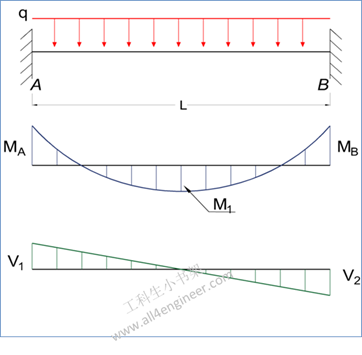
图 2
2.1 弯矩计算
MA = – q L2 / 20
式 7
- MA =固定端A的力矩(Nm)
- q =均匀下降载荷(N / m)
MB = – q L2 / 30
式 8
- MB =固定端B的力矩(Nm)
M1 = q L2 / 46.6
式 9
- M1 = 0.475 L(Nm)时的力矩
2.2 挠度计算
δmax = q L4 / (384 E I)
式 10
- δmax=中心的最大挠度(m)
- E =弹性模量(Pa(N / m2),N / mm2,psi)
- I =惯性面积矩(m4,mm4)
2.3 支反力计算
RA = RB
= q L / 2
式 11
- R =固定端的支反力(N)
3 简支梁梯形分布载荷计算
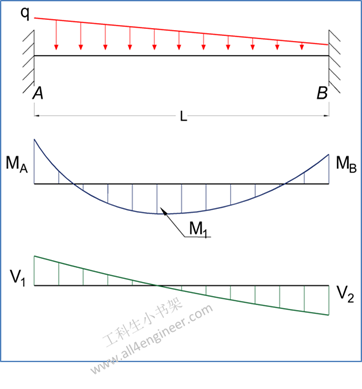
图 3
3.1 弯矩计算
MA = – q L2 / 20
式 12
- MA =固定端A的力矩(Nm)
- q =均匀下降载荷(N / m )
MB = – q L2 / 30
式 13
- MB =固定端B的力矩(Nm)
M1 = q L2 / 46.6
式 14
- M1 = 0.475 L(Nm)时的力矩
3.2 挠度计算
δmax = q L4 / (764 E I)
式 15
- δmax= 0.475 L(m)时的最大挠度
- E =弹性模量(Pa(N / m2),N / mm2,psi)
- I =惯性面积矩(m4,mm4)
δ1/2 = q L4 / (768 E I)
式 16
- δ1/2 = 0.5 L 时的挠度(m)
3.3 支反力计算
RA = 7 q L / 20
式 17
- RA =固定端A的支反力(N)
RB = 3 q L / 20
式 18
- RB =固定端B的支反力(N)
4 简支梁部分均匀的连续分布载荷计算
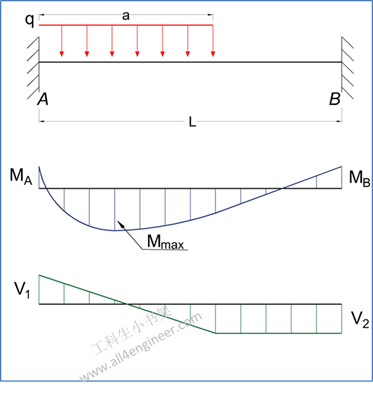
图 4
4.1 弯矩计算
MA = – (q a2 / 6) (3 – 4 a / l + 1.5 (a / L)2)
式 19
其中:
- MA =固定端A的力矩(Nm)
- q =部分均匀载荷(N / m )
MB = – (q a2 / 3) (a / L – 0.75 (a / L)2)
式 20
- MB =固定端B的力矩(Nm)
4.2 支反力计算
RA = q a (L – 0.5 a) / L – (MA – MB) / L
式 21
其中:
- RA =固定端A的支反力(N)
RB = q a2 / (2 L) + (MA – MB) / L
式 22
- RB =固定端B的支反力(N)
