
1 长柱单元的屈曲计算
当外载荷达到临界载荷F时,柱单元会因屈曲效应而失效。
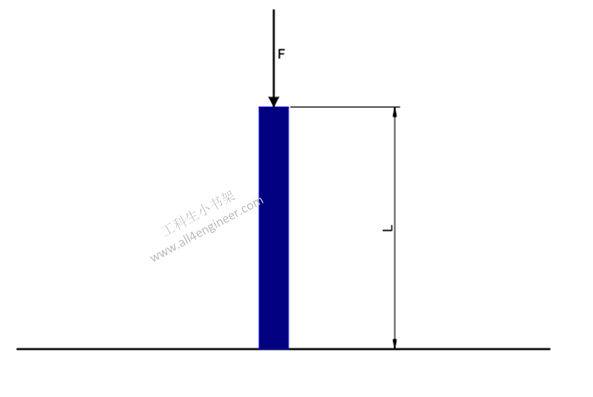
长柱单元可以使用欧拉柱公式进行分析:
F = n π2 E I / L2
式 1
其中:
- F = 允许的最大载荷 (N)
- n = 柱单元的约束系数
- E = 杨氏模量 (Pa (N/m2))
- L = 柱单元的长度 (m)
- I = 柱单元的截面惯惯性矩 (m4)
2 柱单元的边界条件系数
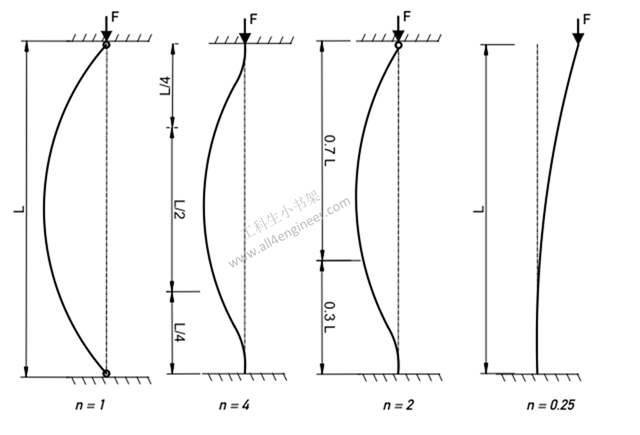
- 两端可旋转:n = 1
- 两端固定:n = 4
- 一端固定,另一端可旋转:n = 2
- 一端固定,一端自由:n = 0.25
有的时候也用K代替n来描述边界条件:
k = (1 / n)1/2
式 2
K-n 转换表:
| n | 1 | 4 | 2 | 0.25 |
| K | 1 | 0.5 | 0.7 | 2 |
因此最大允许载荷可以表示为:
F = π2 E I / (K L)2
式 3
注意:需要注意的是以上公式为长柱单元的计算方式。
工程上用柱单元的细长比来判断长短性质。
- 短柱是细长比不超过50的柱;
- 中长柱的细长比在50到200范围内,其失效模式受材料强度极限约束;
- 长柱的细长比大于200,失效模式受材料的弹性模量约束。
3 细长比(slenderness ratio)
柱单元的有效长度相对于截面积最小回转半径的比例,称为细长比λ(slenderness ratio)
λ=KL/r
式 4
其中:
- K=柱单元边界条件系数(如上表所示)
- L=柱单元有效长度(m)
- r=回转半径(m)
3.1 回转半径(Radius of Gyration)
回转半径r(Radius of Gyration)表示弯曲处距截面质心的距离,在该距离处所有区域都可以集中而对惯性矩没有任何影响。形状相对于每个轴的回转半径由下式给出:
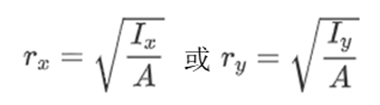
其中:
- Ix=柱单元截面相对于X轴的惯性矩(m4)
- Iy=柱单元截面相对于Y轴的惯性矩(m4)
- A=截面面积((m2)
