1 悬臂梁的单点载荷计算
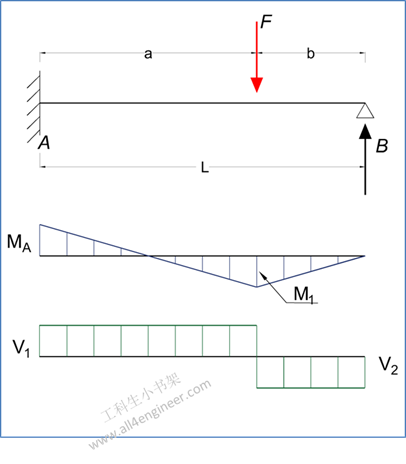
图 1
1.1 弯矩计算
MA = – F a b (L + b) / (2 L2)
式 1
其中:
MA =固定端A的力矩(Nm)
F = 载荷 (N)
MF = Rb b
其中:
- MF =负载点F的力矩(Nm)
- Rb =支撑B处的支反力(N)
1.2 挠度计算
δF = F a3 b2 (3 L + b) / (12 L3 E I)
式 2
其中:
- δmax=挠度(m)
- E =弹性模量(Pa(N / m2),N / mm2,psi)
- I =惯性面积矩(m4,mm4)
1.3 支反力计算
RA = F b (3 L2 – b2) / (2 L3)
式 3
RA =固定端A的支反力(N)
RB = F a2 (b + 2 L ) / (2 L3)
式 4
- RB =固定端B的支反力(N)
2 悬臂梁的均布载荷计算
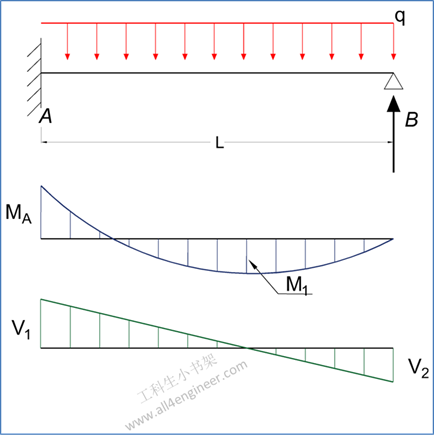
图 2
2.1 弯矩计算
MA = – q L2 / 8
式 5
其中:
- MA =固定端A的力矩(Nm)
- q = 均布载荷 (N/m)
M1 = 9 q L2 / 128
式 6
其中:
- M1 = 0.625 L(Nm)时为最大弯矩
2.2 挠度计算
δmax = q L4 / (185 E I)
式 7
其中:
- δmax= 0.579 L(Nm)时为最大挠度
δ1/2 = q L4 / (192 E I)
式 8
- δ1/2 = L / 2 (m) 的挠度
2.3 支反力计算
RA = 5 q L / 8
式 9
- RA =固定端A的支反力(N)
RB = 3 q L / 8
式 10
- RB =固定端B的支反力(N)
3 悬臂梁的梯形载荷计算
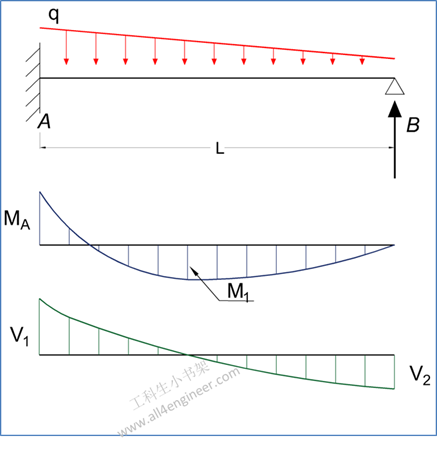
图 3
3.1 弯矩计算
MA = – q L2 / 15
式 11
其中:
- MA =固定端A的力矩(Nm)
- q = 梯形载荷 (N/m)
M1 = q L2 / 33.6
式 12
其中:
- M1 = 0.553 L(Nm)时为最大弯矩
3.2 挠度计算
δmax = q L4 / (419 E I)
式 13
其中:
- δmax= 0.553 L(Nm)时为最大挠度
δ1/2 = q L4 / (427 E I)
式 14
- δ1/2 = L / 2 (m) 的挠度
3.3 支反力计算
RA = 2 q L / 5
式 15
- RA =固定端A的支反力(N)
RB = q L / 10
式 16
- RB =固定端B的支反力(N)
4 悬臂梁的附加弯矩计算
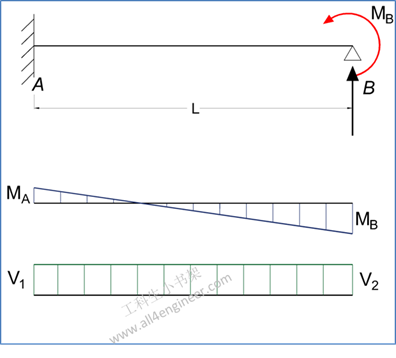
图 4
4.1 弯矩计算
MA = -MB / 2
式 17
其中:
- MA =固定端A的力矩(Nm)
4.2 挠度计算
δmax = MB L2 / (27 E I)
式 18
其中:
- δmax = 2/3 L (m)为最大挠度
4.3 支反力计算
RA = 3 MB / (2 L)
式 19
- RA =固定端A的支反力(N)
RB = – 3 MB / (2 L)
式 20
- RB =固定端B的支反力(N)
