1 体积模量
体积模量(K)也称为不可压缩量,是材料对于表面四周压强产生形变程度的度量。它被定义为产生单位相对体积收缩所需的压强。它在SI单位制中的基本单位是Pa,即帕斯卡。
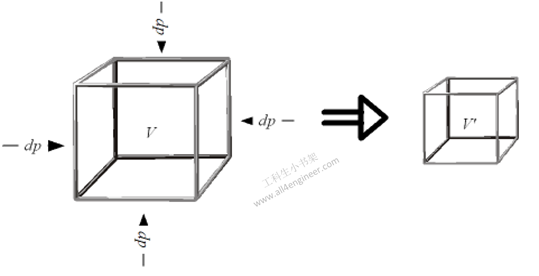
体积模量可以用下式计算:

体积模量的另一种形式:

当压强增大,体积变小,即密度增大。更大的体积模量意味着液体的不可压缩性。
2 某些常见流体的体积模量
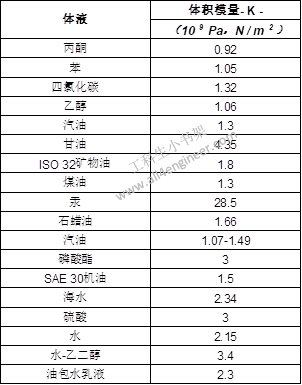
注:1 GPa = 109 Pa(N / m 2)
不锈钢的体积模量大约为163×109 Pa,水的体积模量2.15×109 Pa,因此不锈钢比水难压缩80倍。
体积模量(K)也称为不可压缩量,是材料对于表面四周压强产生形变程度的度量。它被定义为产生单位相对体积收缩所需的压强。它在SI单位制中的基本单位是Pa,即帕斯卡。

体积模量可以用下式计算:

体积模量的另一种形式:

当压强增大,体积变小,即密度增大。更大的体积模量意味着液体的不可压缩性。

注:1 GPa = 109 Pa(N / m 2)
不锈钢的体积模量大约为163×109 Pa,水的体积模量2.15×109 Pa,因此不锈钢比水难压缩80倍。
体积模量 (Bulk Modulus)也称为不可压缩量,是材料对于表面四周压强产生形变程度的度量。它被定义为产生单位相对体积收缩所需的压强。单位为:Pa(N/m2)
其计算公式为:
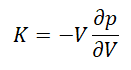
式 1
其中:
体积模量的倒数即为一种物质的压缩率。
体积模量的倒数即为一种物质的压缩率。体积模量和拉伸模量、泊松比之间有关系:
E = 3K(1-2μ)
式 2
其中:
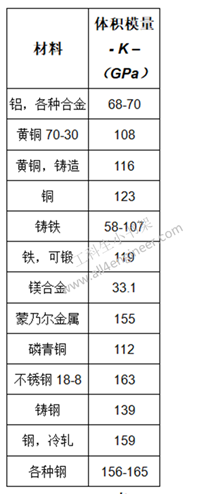
注:1 GPa = 109 Pa (N/m2)
杨氏模量也称杨氏模数(英语:Young’s modulus),一般将杨氏模量习惯称为弹性模量。弹性材料承受正向应力时会产生正向应变,在形变量没有超过对应材料的一定弹性限度时(符合胡克定律阶段),定义正向应力与正向应变的比值为这种材料的杨氏模量。其公式为:
E = 应力 / 应变
= σ / ε
= (F / A) / (dl / l0)
式 1
其中:
剪力模数(shear modulus)定义为剪应力与剪应变的比值
G = stress / strain
= τ / γ
= (Fp / A) / (s / d)
式 2
其中:
在均质且等向性的材料中:
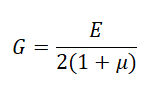
式 3
其中:
体积模量 (Bulk Modulus)也称为不可压缩量,是材料对于表面四周压强产生形变程度的度量。它被定义为产生单位相对体积收缩所需的压强。单位为:Pa(N/m2)
其计算公式为:
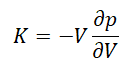
式 4
其中:
体积模量的倒数即为一种物质的压缩率。
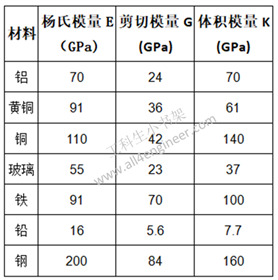
注:1 GPa = 109 Pa (N/m2)