1  皮带传动的功率和效率的计算方法

以上图为例，从动轮A上的扭矩可以用下式计算：

T = (F₂ – F₁) r_a

其中：

• T = 扭矩 (Nm)
• F = 力 (N)
• r = 皮带轮半径 (m)

1.1  皮带传动有效功率的计算公式：

P = T ω_a = (F₂ – F₁) r_a ω_a

其中：

• P = 传递的有效功率(w，瓦特)
• ω_a = 角速度 (rad/s，弧度/秒)

1.2  皮带传动效率的计算公式：

η = P_A/P_B= (F₂ – F₁) r_a ω_a/P_B

其中：

• η = 皮带传动效率（%）
• P_A = 传递的有效功率(w，瓦特)
• P_B = 来自电机或发动机的输出功率(w，瓦特)

直线度是表示零件上的直线要素保持理想直线的状态，即通常所说的平直程度。直线度公差是实际线对理想直线所允许的最大变动量。无基准要求。

1  直线度调用形式

直线度在GD＆T中实际上有两个非常不同的功能，具体取决于其调用方式。 一种是作为表面直线度（Surface Straightness），控制表面或特征上某处线条的形式的公差。 另一种是作为轴心线直线度（Axis Straightness），它控制零件轴上允许的曲线数量。 通常调用时会包含最大实体要求。 两种用法完全不同！

图左：表面直线度；                        图右：轴心线直线度

2  基本描述

表面直线度：

标准形式是二维公差。用于确保零件在整个表面或特征上均匀。表面直线度可以应用于平面特征（例如块的表面），也可以沿轴向方向应用于圆柱体的表面。它定义为该表面上指定线内的表面公差。

轴心线直线度：

控制零件中心轴的直线度。轴心线直线度公差实际上是3D公差，它约束零件的中心轴，防止其弯曲或扭曲太多。

当最大实体要求应用于轴心线直线度公差时，其给出的公差值是在该要素处于最大实体状态下的。当被测要素的实际轮廓偏离其最大实体状态，即其实际尺寸偏离最大实体尺寸时，形位公差值可以超出在最大实体状态下给出的形位公差值，即此时的形位公差值可以增大。

3  公差带

表面直线度：距离为公差值0.03mm的两平行线之间的区域。

轴心线直线度：公差带是圆柱形区域。被测元素的实际轴线必须位于该直径为t的圆柱面内。（最大实体要求下， 尺寸公差可以对形位公差值进行补偿，附加公差= 最大实体尺寸与零件实际尺寸之间的差。）。

表面直线度公差带

轴心线直线度公差带

4  测量

表面直线度：零件固定，量规沿直线测量。测量高度的变化可以看出直线沿该表面的平直度。

轴心线直线度：为确保零件或特征在轴向上是直的，使用了一个圆柱测量工具来确定零件是否位于最大实体状态下的总包络线内。 这既控制了直径，也控制了轴的直线度。

计算梁的载荷和支反力，如下图：

1  力的方程：

F₁ + F₂ + …. + F_n = R₁ + R₂ 

2  力矩的方程：

F₁ a_f1 + F₂ a_f2 + …. + F_n a_fn = R a_r1 + R a_r2 

• F = 载荷 (N)
• R = 支反力 (N)
• a = 载荷距支点的距离，通常选择其中一个支点为原点 (N)

联立上面2式可得支反力：R1和R2

1  拱的分类

最常见的几种拱为固定拱、两铰拱（two-hinged arch）及三铰拱（three-hinged arch）。

1.1  固定拱

固定拱最常用在跨度较小的钢筋混凝土桥以及隧道。固定拱需承受内部结构因为温度变化产生的热胀冷缩，因此是静不定结构。

1.2  两铰拱

两铰拱（two-hinged arch）最常用在大跨度的桥。这种拱在其拱的底座是由铰支承固定旳，和固定拱的底座不同，铰支承可以旋转，让结构可以形变，以配合因为室外温度变化产生的热胀冷缩。不过仍然会有额外的应力，因此两铰拱仍然是静不定拱，不过情形比固定拱要好很多。

1.3  三铰拱

三铰拱（three-hinged arch）不止在底座有铰支承固定，在其顶点也有铰支承固定。因此可以在水平及垂直的方向变形，以配合因为室外温度变化产生的热胀冷缩。这种拱没有因为热胀冷缩产生的应力，因此是静定结构。三铰拱最常用在中等跨距的拱，例如大型建筑的屋顶。三铰拱的另一个好处是铰支承底座比固定式底座好施工，可以在中等长度范围内使用浅的，轴承型基础。在三铰拱中，拱的热热胀冷缩会让顶点有垂直方向的位移，但二个底座不会有太大的影响，这可以简化底座的设计。

2  均布载荷下的三铰拱计算

2.1  弯矩计算

M_m = (q L² / 8) (4 (x_m / L – (x_m / L)²) – y_m / y_c)

其中：

• M_m = m点处的弯矩 (Nm)
• q = 均布载荷 (N/m)
• x_m = m点的x轴坐标 (m)
• y_m = m点的y轴坐标 (m)
• y_c = 中间铰接点的y轴坐标(m)
• L = 拱的跨度(m)

2.2  支反力

R_1y = R_2y

= q L / 2

其中：

• R_y = y向支反力 (N)

R_1x = R_2x

= q L² / (8 y_c)

其中：

• R_x = x向支反力 (N)
• y_c = 中间铰接点的y轴坐标(m)

3  部分均布载荷下的三铰拱计算

3.1  弯矩计算

M_m = (q L² / 16) (8 (x_m / L – (x_m / L)²) – 2 x_m / L  – y_m / y_c)  

其中：

• M_m = m点处的弯矩 (Nm)
• q = 均布载荷 (N/m)
• x_m = m点的x轴坐标 (m)
• y_m = m点的y轴坐标 (m)
• y_c = 中间铰接点的y轴坐标(m)
• L = 拱的跨度(m)

3.2  支反力计算

R_1y = 3 q L / 8

R_2y = q L / 8

R_1x =  R_2x= q L² / (16 y_c)

4  点载荷下的三铰拱计算

4.1  弯矩计算

M_m = (F a / 2) (2 (b / a) (x_m / L) – y_m / y_c)

M_k = (F a /2) (2 (L – x_k) / L – y_k / y_c)  

4.2  支反力

R_1y = F b / L

R_2y = F a / L

R_1x = R_2x= F a / (2 y_c)

其中：

• M_k = k点处的弯矩 (Nm)
• F = 点载荷 (N)

当薄壁管或罐受到内压时，管壁上会产生纵向应力和径向（或环向）应力。

通常认为壁厚小于管道直径的1/20时，认为是薄壁管道，适用于以下计算：

1  轴向应力

对于两端都封闭的气缸，内部压力会沿着气缸的轴线产生一个力。由该力引起的纵向应力可以计算为

σ_l = p d / (4 t)

其中：

• σ_l = 轴向应力(MPa)
• p = 管道内部压强 (MPa)
• d = 管道内径 (mm)
• t = 管道壁厚 (mm)

2  环向应力

环向应力沿圆周方向作用，并垂直于圆柱壁的轴线和半径。环向应力可以计算为

σ_h = p d / (2 t)  

其中：

• σ_h = 环向应力 (MPa)
• p = 管道内部压强 (MPa)
• d = 管道内径 (mm)
• t = 管道壁厚 (mm)

注意：一般碳钢管的最大允许应力低于135 MPa。

1  长柱单元的屈曲计算

当外载荷达到临界载荷F时，柱单元会因屈曲效应而失效。

长柱单元可以使用欧拉柱公式进行分析：

F = n π² E I / L²

式 1

其中：

• F = 允许的最大载荷 (N)
• n = 柱单元的约束系数
• E = 杨氏模量 (Pa (N/m²))
• L = 柱单元的长度 (m)
• I = 柱单元的截面惯惯性矩 (m⁴)

2  柱单元的边界条件系数

• 两端可旋转：n = 1
• 两端固定：n = 4
• 一端固定，另一端可旋转：n = 2
• 一端固定，一端自由：n = 0.25

有的时候也用K代替n来描述边界条件：

k = (1 / n)^1/2

式 2

K-n 转换表：

n	1	4	2	0.25
K	1	0.5	0.7	2

因此最大允许载荷可以表示为：

F = π² E I / (K L)²

式 3

注意：需要注意的是以上公式为长柱单元的计算方式。

工程上用柱单元的细长比来判断长短性质。

• 短柱是细长比不超过50的柱；
• 中长柱的细长比在50到200范围内，其失效模式受材料强度极限约束；
• 长柱的细长比大于200，失效模式受材料的弹性模量约束。

3  细长比（slenderness ratio）

柱单元的有效长度相对于截面积最小回转半径的比例，称为细长比λ（slenderness ratio）

λ=KL/r

式 4

其中：

• K=柱单元边界条件系数（如上表所示）
• L=柱单元有效长度（m）
• r=回转半径（m)

3.1  回转半径（Radius of Gyration）

回转半径r（Radius of Gyration）表示弯曲处距截面质心的距离，在该距离处所有区域都可以集中而对惯性矩没有任何影响。形状相对于每个轴的回转半径由下式给出：

其中：

• I_x=柱单元截面相对于X轴的惯性矩（m⁴)
• I_y=柱单元截面相对于Y轴的惯性矩（m⁴)
• A=截面面积（（m²)

桁（héng）架（英文：truss）

桁架简单地定义为构件的三角剖分，以形成稳定的结构。三角剖分是数学上的稳定配置。通常桁架具有称为上弦，下弦，垂直弦和对角弦的单元。桁架的主要功能：

• 从上方结构承载载荷
• 为整个结构提供足够的横向稳定性

在设计过程中有一些基本假设。应该明确的是，桁架的构造应符合设计假设，以避免由于力和载荷的分散而引起的不必要的破坏。以下是桁架设计和计算中的基本假设：

1. 桁架结构单元仅承受轴向力（及轴向拉压载荷）
2. 节点（即单元的连接）被设计为胶接，从而不会将力矩传递给桁架杆单元
3. 所有外部负载和反应仅作用于节点上
4. 通常情况下桁架应在同一平面上。
5. 通常情况下将桁架的构件制成I形，三角形，T形，管形，方形和槽形。就结构分析结果而言，I型截面更适合作为优化截面。

1  桁架类型

1.1  简易桁架

三角形就是最简单的桁架，这类的桁架常出现在屋顶，由二根斜向的椽架及水平的托梁组成一个单元，像在自行车及飞机上也可以看到类似的架构。这类的桁架有形状的稳定性，且已有方法可以分析其各部分的受力，因此由三角形组成的桁架称为简易桁架。像传统由二个相邻三角形组成的钻石型自行车车架，就是简易桁架的例子。

1.2  平面桁架

平面桁架位在同一平面上，一般会用数个平面桁架平行排列，组成屋顶及桥梁。

平面桁架的深度，也就是平面桁架上方及下方的上弦杆及下弦杆之间的距离，是桁架之所以成为经济耐用的结构的原因。实心的梁或是梁不论是重量或是成本，都比相同强度的桁架要贵。跨度相同时，若桁架的深度越深，其上弦杆及下弦杆所需的材料越少，但垂直杆及对角线杆需要的材料会增加。因此若深度最佳化，桁架的成本也可以节省。

1.3  立体桁架

空间桁架是三维的框架，各杆的末端以旋转接点相接。四面体的外形是最简单的桁架，由六根杆组成，有四个接点。大型的平面结构也可以用四面体组成，在大型的独立输电杆塔中也有用到立体桁架。

四面体桁架

2  平面桁架的常见类型

2.1  普拉特桁架

普拉特桁架 普拉特桁架（Pratt truss）是由二位波士顿铁路工程师在1844年申请专利。其设计用垂直杆件来承受压缩力，水平垂直杆件来承受张力，现今这仍是常用的桁架型式，只是原有的木头换成铁，最后再换成钢。普拉特桁架持续受欢迎的原因也许也因为较长的对角杆件只承受因为重力效应产生的张力，因为对角细长杆件若承受压力下，比较容易会挫曲，这在设计上也不易控制。因为若针对固定深度的平面桁架，承受静态、垂直的荷重，普拉特桁架也许是最有效的桁架。

2.2  弓弦桁架

弓弦桁架（Bowstring truss）因其外型得名，最早用在有拱的桁架桥，常和系拱桥混淆。弓弦桁架桥的桥拱和桥面是以杆件相连，而系拱桥是用绳索或钢索连接桥拱和桥面。

在二次大战时时兴建了上千座弓弦桁架，目的是为了飞机库或是其他军用建筑的曲线。连结上弦杆和下弦杆之间的杆有许多不同的变化，从接近等腰三角形到类似普拉特桁架的变体。

2.3  单柱桁架

单柱桁架（king post truss）是桁架中最简单的一种，有一个垂直的柱子支撑，两侧则有斜的杆件。

2.4  双柱桁架

双柱桁架（queen post truss）类似单柱桁架，但中间是二根垂直柱子，之间用梁连接，以提供其结构稳定性，这类桁架只适用在跨距较短的应用中。

2.5  透镜桁架桥

透镜桁架桥（Lenticular trusses）是由威廉·道格拉斯在1878年申请专利 ，不过1823年的Gaunless桥是第一座透镜桁架桥，其上弦板及下弦板都是拱形的，因此整体像透镜一样。

2.6  格构桁架

美国建筑师 Ithiel Town设计了格构桁架，取代用粗重木头作的桥，他的设计在1820年及1835年申请专利，利用易于处理的木板，对角线的固定在上弦板及下弦板之间。

当厚壁管或圆柱体受到内部和外部压力时，壁中会产生轴向，径向，和法向应力。

1  轴向应力

管壁某一点某一点的轴向应力可以表示为：

σ_a = (p_i r_i² – p_o r_o² )/(r_o² – r_i²)

其中：

• σ_a = 轴向应力 (MPa)
• p_i = 管道内部压力 (MPa)
• p_o = 管道外部压力 (MPa)
• r_i = 管道内壁半径 (mm)
• r_o =管道外壁半径 (mm)

2  环向应力

管壁某一点的圆周方向应力（环向应力）可以表示为：

σ_c = [(p_i r_i² – p_o r_o²) / (r_o² – r_i²)] – [r_i² r_o² (p_o – p_i) / (r² (r_o² – r_i²))]

其中：

• σ_c = 管道圆周切线方向的应力 (MPa)
• r = 管道壁计算点的半径 (mm) (r_i < r < r_o)，当 r = r_i (内壁半径)时，环向应力最大

3  法向应力

管壁上某一点的法向应力可以表示为：

σ_r = [(p_i r_i² – p_o r_o²) / (r_o² – r_i²)] + [r_i² r_o² (p_o – p_i) / (r² (r_o² – r_i²))]

• 当 r = r_o (外壁半径)时，法向应力最大

4  计算注意事项

• 以上三个方向的应力不可直接用笛卡尔直角坐标系向量叠加方法求出主应力大小和方向，而是要采用圆柱坐标系的来计算
• 除了压力膨胀应力，在管道内部的气体或液体由于压力作用引起的温度变化，进而引入的热膨胀应力，同样是计算过程中不可忽略的因素。热膨胀应力计算参考工科生小书架文章：热膨胀及应力计算

1  谐波振荡器

可以将简单的谐波运动用作各种运动（例如弹簧的振动）的数学模型。

简单谐波振荡器的时间周期可以表示为：

T = 2 π (m / k)^1/2

• T = 时间 (s)
• m = 质量 (kg)
• k = 弹簧的强度系数 (N/m)

2  算例-简单谐波振荡器的震荡周期

500 kg的质量连接到弹簧常数为16000 N / m的弹簧上。震荡周期可以计算为：

T = 2π（（500kg）/（16000 N / m））^1/2

  = 1.1s

1  胡克定律

胡克定律/虎克定律(Hooke’s law)，是力学弹性理论中的一条基本定律，内容：固体材料受力后，应力与应变(单位变形量)成线性关系，满足此定律的材料：线弹性/胡克型(Hookean)。从物理的角度看，胡克定律源于多数固体(或孤立分子)内部的原子在无外载作用下处于稳定平衡的状态。

胡克定律应用的一个常见例子是弹簧。在弹性限度内，弹簧的弹力F和弹簧的长度变化量s成线性关系，拉伸或压缩弹簧所需的力可以用胡克定律表示为

F = – k s

• F = 力 (N)
• k  = 弹簧强度系数 (N/m)
• s = 弹簧长度变化 (m)

2  胡克定律的广义变化

在胡克定律的广义变化中，它指出弹性物体或材料的应变/变形与施加于其上的应力成比例。它可以用数学表示为

σ= Eε

其中：

• σ=应力（Pa）
• E =杨氏弹性模量（Pa）
• ε=应变（m / m）

胡克定律仅适用于特定加载条件下的部分材料。钢材在多数工程应用中都可视为线弹性材料，在弹性范围内（即应力低于屈服强度时）胡克定律都适用。另外一些材料（如铝材）则只在弹性范围内的一部分区域行为符合胡克定律。对于这些材料需要定义一个应力线性极限，在应力低于该极限时线性描述带来的误差可以忽略不计。

还有一些材料在任何情况下都不满足胡克定律（如橡胶），这种材料称为“非胡克型”（neo-hookean）材料。橡胶的刚度不仅和应力水平相关，还对温度和加载速率十分敏感。

胡克定律在磅秤制造、应力分析和材料模拟等方面有广泛的应用。

1  飞轮简介

飞轮（flywheel）是指转动惯量很大的零部件，可用于消除能量波动，并使间歇运行的能量流更均匀。能量以动能的形式存储在飞轮中。内燃机飞轮是最为常见的飞轮应用，一个活塞式的四冲程发动机，除了做功行程，其它的三个进气、压缩和排气行程都要靠飞轮储存的能量来维持旋转。

2 飞轮中存储的动能

E_f = 1/2 I ω²

• E_f = 飞轮种存储的动能 (Nm, J)
• I = 飞轮的转动惯量 (kg m²)
• ω = 飞轮的角速度 (rad/s)

角速度的角度-弧度转换：

1 rad = 360° / 2 π =~ 57.29578°

1 rad/s = 9.55 转/min (rpm) = 0.159 转/s (rps)

• rpm=round per minute 即：转/分
• rps= round per second 即：转/秒

转动惯量I可以表示为:

I = k m r²

其中：

• k = 转动惯量系数–取决于飞轮的形状
• m = 飞轮质量 (kg)
• r = 飞轮半径 (m)

几种常见飞轮的惯性常数

• 轮辋像自行车轮胎一样装在轮辋上-k = 1
• 厚度均匀的扁平实心圆盘-k = 0.606
• 带中心孔的平盘-k =〜0.3
• 实心球-k = 2/5
• 薄边-k = 0.5
• 径向杆-k = 1/3
• 圆形刷子-k = 1/3
• 薄壁空心球-k = 2/3
• 细矩形杆-k = 1/2

3  算例示例-旋转自行车车轮中的能量

典型的26英寸自行车轮辋的直径为559mm，轮胎外径约为665mm（26.2英寸）。为了方便计算，将车轮的半径-r-近似为

r =（（665mm）+（559mm）/ 2）/ 2

  = 306 mm

  = 0.306 m

车轮的重量为2.3 kg，惯性常数为k = 1。

可以计算出车轮的惯性矩

I =（1）（2.3 kg）（0.306 m）² 

   = 0.22 kg m²

自行车的速度为25 km / h（6.94 m / s）。车轮圆周速度（rps即转/ s）-n _rps- 可以计算为

n _rps =（6.94 m / s）/（2π（0.665 m）/ 2）

     = 3.32转/ s

车轮的角速度可以计算为

ω=（3.32转/s）（2π rad/转）

   = 20.9 rad/ s

然后可以计算出旋转的自行车车轮的动能为

E _f = 0.5（0.22 kg m ²）（20.9 rad / s）²     

  = 47.9 焦耳

1  角度弧度的转换

人们通常习惯于角度数的计算，即一周为360°，而在弧度通常以计算机语言使用。

由360°=2 π，可以推导出下式：

θ = 2 π Φ / 360

• θ = 弧度
• Φ = 角度

将上式变换一下：

Φ = 360 θ / (2 π)

• θ = 弧度
• Φ = 角度

2  0-360度的弧度值

角度	弧度
0	0
10	0.174533
20	0.349066
30	0.523599
40	0.698132
50	0.872665
60	1.047198
70	1.22173
80	1.396263
90	1.570796
100	1.745329
110	1.919862
120	2.094395
130	2.268928
140	2.443461
150	2.617994
160	2.792527
170	2.96706
180	3.141593
190	3.316126
200	3.490659
210	3.665191
220	3.839724
230	4.014257
240	4.18879
250	4.363323
260	4.537856
270	4.712389
280	4.886922
290	5.061455
300	5.235988
310	5.410521
320	5.585054
330	5.759587
340	5.934119
350	6.108652
360	6.283185

1  均布载荷下线缆的支反力和张力

1.1  线缆均布载荷的支反力计算

可以将载荷均匀分布的中跨电缆和水平支撑力计算为:

R_1x = R_2x = R_x = q L² / (8 h)

式 1

• R_1x = R_2x = R_x = 端座支反力的水平分量  (N)
• q = 均布载荷–一般为重力 (N/m)
• L = 跨度 (m)
• h = 垂度 (m)

R_1y = R_2y = R_y = q L / 2

式 2

• R_1y = R_2y = R_y = 端座支反力的垂直分量 (N)

T_max = (R_x² + R_y²)^0.5

式 3

• T_max=支撑处的合力（N）–方向为线缆在支撑处的切线方向

电缆的长度S可以近似为：

S = L + 8 h² / (3 L)

式 4

2  高低底座的均布载荷线缆的计算

负载均匀分布的水平电缆和支撑力可以计算为：

R_1x = R_2x = R_x = q L² / (8 h)

式5

电缆末端的垂直支反力可以计算为：

R_1y = R_2y = R_y = R_x d / L + q L / 2

式6

作用在支撑端的合力（方向为线缆在支撑处的切线方向）可以计算为：

T_max = (R_x² + R_y²)^0.5

式7

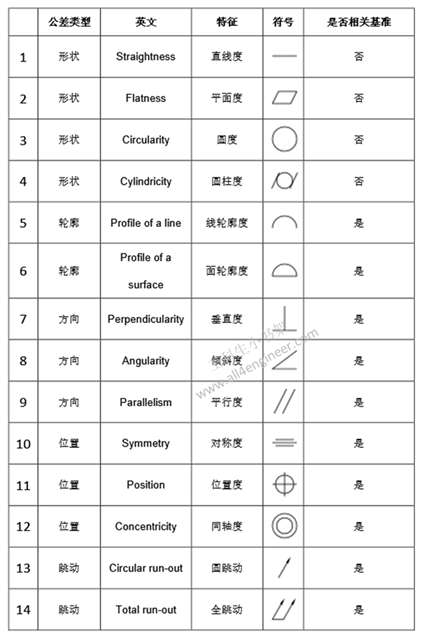
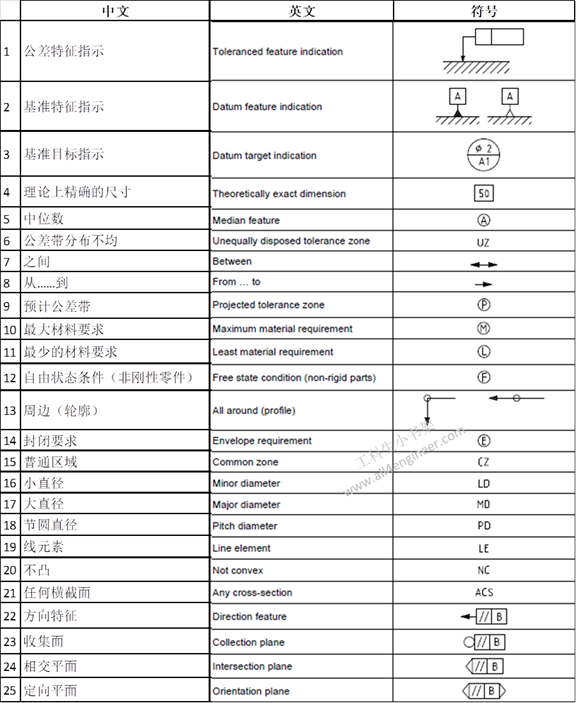
1  形位公差符号详解

1.1  直线度

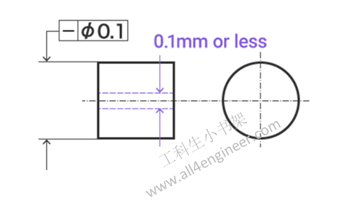
直线度要求指定目标应达到的完美直线度。它应用于线而不是平面，并表示中心线或母线中的曲线。 因此，直线度用于表示长物体的翘曲公差。

图例解释：如果公差框架连接到指示圆柱体直径的尺寸，则该圆柱体的轴线必须位于直径为0.1 mm的圆柱体内。

1.2  平面度

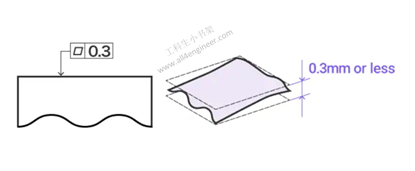
平整度要求指定了表面的平整度或目标平面应具有的平整度。 最凸出的部分和最凹入的部分必须在垂直分开的两个平面之间有特定的距离。

图例解释：该表面必须位于两个平行平面之间，且彼此之间仅相隔0.3毫米。

1.3  圆度

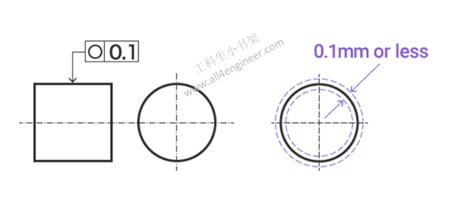
圆度要求指定目标应达到多完美的圆形（轴，孔或圆锥的圆形横截面）。

垂直切割的轴的任何横截面的外圆周应在同一平面上仅相距0.1 mm的两个同心圆之间。

1.4  圆柱度

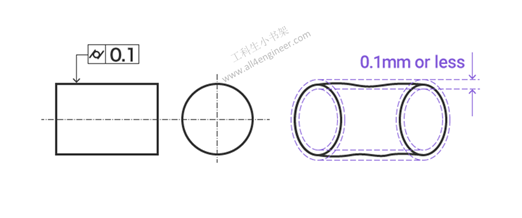
圆柱度要求指定目标圆柱体的圆形和笔直度。 该值表示圆柱体中的任何变形。

图例解释：目标平面必须位于相距0.1 mm的两个同轴圆柱体之间。

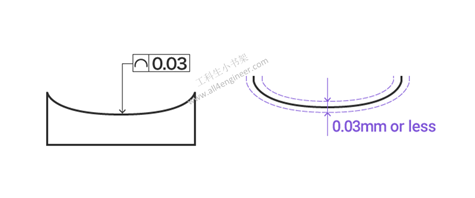
1.5  线轮廓度

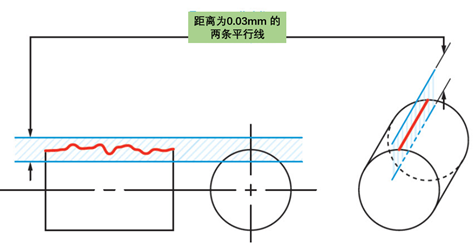
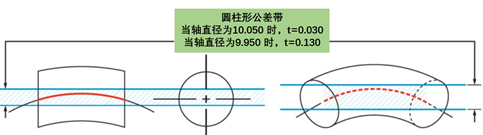
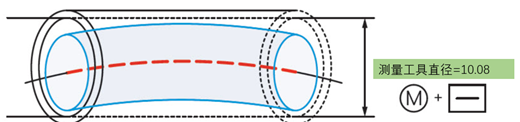
线条要求的轮廓指示是否根据设计来设计零件的曲率。该值指示轮廓线（出现在曲面横截面上的线元素）中的任何变形。跨过指定曲率的横截面线必须在公差带内。

图例解释：在平行于投影平面的任何横截面上，目标轮廓必须位于两个包络之间，该两个包络由直径为0.03 mm的圆和理论上精确轮廓的直线上的中心为中心。

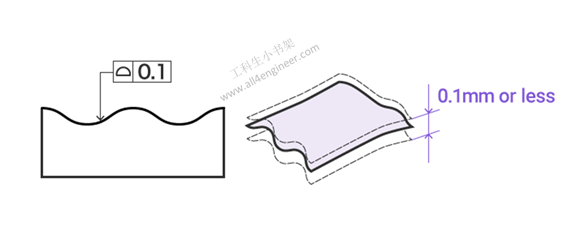
1.6  面轮廓度

平面要求的轮廓指示是否根据设计来设计零件的曲率（表面）。与直线的轮廓公差不同，平面的轮廓公差涉及整个指定的曲率。

图例解释：目标平面必须位于两个直径为0.1 mm的球体所形成的包络平面之间，并且该平面的中心具有理论上精确的轮廓。

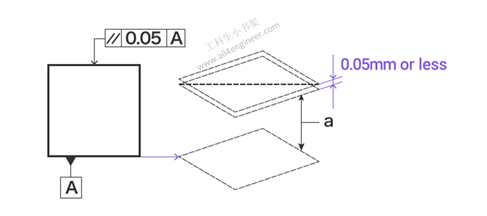
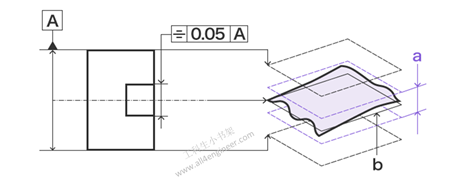
1.7  平行度

虽然它看起来与平面度相似，但平行度涉及一个基准（参考平面或基准线）。平行度要求指定两条线或平面平行。

图例解释：指示箭头指示的平面必须平行于基准平面A，并且在指示箭头方向上仅相距0.05 mm的两个平面之间。

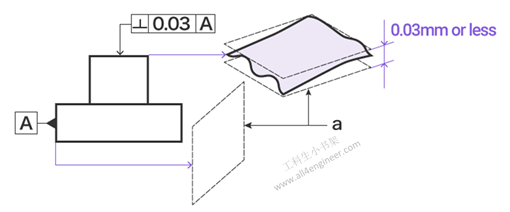
1.8  垂直度

垂直度要求指定目标与基准（参考平面或直线）垂直度的精度。替度，而是使用毫米作为垂直度指示值的单位。

图例解释：指示箭头指示的平面必须在垂直于基准平面A的圆柱体内，并且误差不超过0.03毫米。

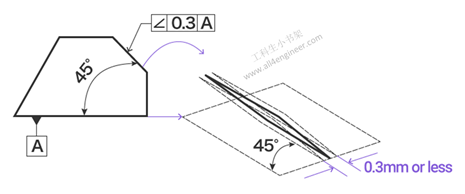
1.9  倾斜度

角度要求指定当指定的线或平面不是90度时，与基准（参考平面或线）的角度的精确度。替代度数，将毫米用作角度指示值的单位。

图例解释：指示箭头指示的平面在理论上必须与基准平面A精确地成45度角，并且在两个平行平面之间沿指示箭头的方向仅相距0.3毫米。

1.10  位置度

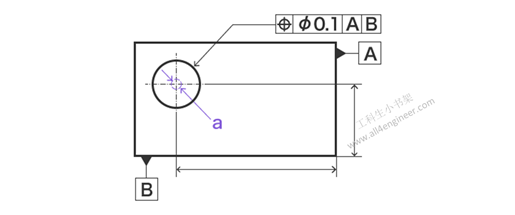
真实位置要求指定相对于基准（参考平面或直线）的位置精度。

图例解释：指示箭头指示的圆心必须在直径为0.1毫米的圆内。

1.11  同轴度（同心度）

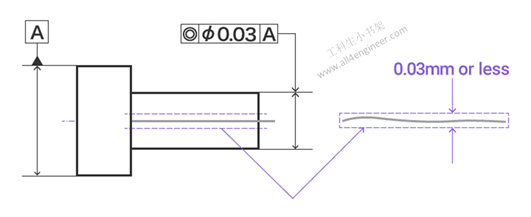
同轴度要求指定两个圆柱体的轴的同轴度（中心轴无偏差）。

图例解释：指示箭头指示的圆柱轴必须位于以基准轴线A为轴且直径误差不超过0.03毫米的圆柱体内。

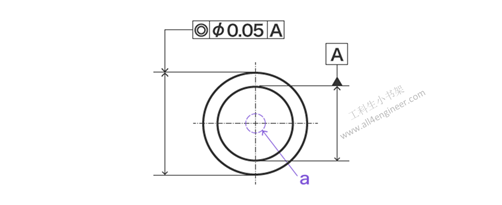
• 同心度要求指定两个圆柱体的轴同心度的精度（中心无偏差）。 与同轴度不同，基准是中心点（平面）。

图例解释：指示箭头指示的圆柱轴必须位于以基准轴线A为轴且直径为0.05毫米的圆柱体内。

1.12  对称度

对称性要求指定目标相对于基准（参考平面）的对称性的精度。

图例解释：指示箭头指示的中心平面必须在两个平行于基准中心平面A的平行平面之间，并且彼此间隔0.05 mm。

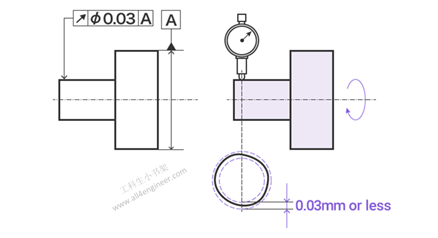
1.13  圆跳动

圆跳动指定旋转零件时圆周的任何部分的跳动。为了满足圆形跳动的要求，零件旋转时测量值的跳动必须在指定范围内。

图例解释：当目标在基准轴线上旋转一次时，圆柱体表面在径向上的跳动（如箭头所示）在垂直于基准轴线的任何测量平面上不得超过0.03 mm。

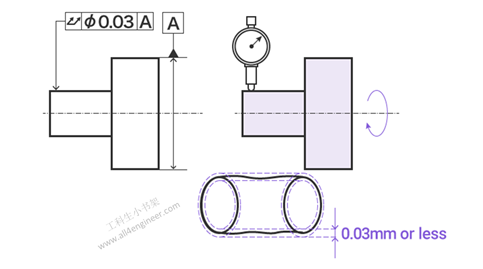
1.14  全跳动

总跳动指定零件旋转时整个零件表面的跳动。为了满足总跳动要求，整个气缸表面的测量值的跳动必须在指定范围内。

图例解释：当圆柱体零件沿基准轴线旋转时，圆柱体表面在径向上的总跳动（如指示箭头所示）在圆柱体表面的任何一点上不得超过0.03 mm。

1  引言

产品零件在加工制造过程中，由于机床精度、刀具夹具及工艺操作水平等因素，零件的尺寸、形状及表面质量、方向和位置均不可能做到完全理想。这种工艺过程中出现的误差有可能会影响到：

• 配合的松紧程度，如圆度，轴线的直线度；
• 可装入性，如螺栓的位置度；
• 零件的其它功能，如工作精度、联接强度、运动平稳性、密封性、耐磨性、可靠性、噪声和使用寿命等。

为了满足零件的使用要求，保证零件的互换性和制造的经济性以及提高设计的通用性，工程师在设计时必须合理控制零件的形位误差，即对零件规定其形状和位置公差（简称形位公差）。

2  形位公差（Geometric Dimensioning and Tolerancing (GD&T)）

形位公差是限制实际被测形体（或要素）变动的区域，是零件的实际形状、位置对其理想形状、位置的变动量。其大小是由指定的形位公差值来确定的。只要被测实际形体（或要素）被包含在这个公差带内，那么这个被测形体（或要素）就是合格的。

形位公差按其控制的要素总共分成如下五大类（共14个）：

	类型	元素
1	形状公差	a. 直线度；b. 平面度；c. 圆度；d. 圆柱度。
2	定向公差	a. 平行度；b. 垂直度； c. 倾斜度。
3	定位公差	a. 同轴度；b. 位置度；c. 对称度。
4	轮廓度公差	a. 线轮廓度；b. 面轮廓度。
5	跳动公差	a. 圆跳动；b. 全跳动。

3  形位公差标准

• 美国标准：ASME Y14.5（ASME Y14.5M）-Dimensioning and Tolerancing
• 国际标准：ISO 1101-Geometrical tolerancing – Tolerances of form, orientation, location and run-out
• 中国国家标准：GB/T1182-产品几何技术规范(GPS)几何公差形状、方向、位置和跳动公差标注

其中：

• GB/T16671 -形状和位置公差 最大实体要求、最小实体要求和可逆要求
• GB/T16892-形状和位置公差 非刚性零件注法
• GB/T17773-形状和位置公差 延伸公差带及其表示法
• GB/T17851-形状和位置公差 基准及基准体系
• GB/T17852-形状和位置公差 轮廓的尺寸及公差注法

三个标准差异不大，ISO和ASME都积极追求标准化，旨在使图纸全球化。中国国家标准GB/T1182大致是根据ISO的翻译而来。

标准下载不到的同学，可以在评论区留下邮箱向工科生小书架|www.all4engineer.com索要。

3.1  形位公差的符号

3.2  附加符号表

1        曲柄连杆机构的计算

曲柄连杆机构将旋转运动转换为往复运动-反之亦然。

图 1

杆端头的位置可以表示为：

s = r (1 – cos φ) + (λ / 2) r sin²φ

式 1

其中：              s = 连杆位置 (m)

r = 曲柄半径 (m)

φ = ω t

   = 2 π n_s t

式 2

其中：ω          = 曲柄角速度 (rad/s)

t        = 时间 (s)

n_s      = 曲柄转速 (转/s)

λ = r / l

式 3

其中：l =杆长（m）

λ = 连杆比

连杆端头速度：

v = ω r sin φ (1 + λ cos φ)

式 4

其中：v = 连杆沿导轨的速度 (m/s)

连杆端头加速度：

a = ω2 r (cos φ + λ cos 2φ) 

式 5

其中：a = 连杆加速度 (m/s²)

1 剪切模量

剪力模数（shear modulus）定义为剪应力与剪应变的比值

2 常用材料的剪切模量

材料	剪切模量 – G -（GPa）
铝合金	27
铝，6061-T6	24
铝，2024-T4	28
铍铜	48
黄铜	40
青铜	44.8
镉	19
碳素钢	77
铸铁	41
铬	115
具体	21
铜	45
玻璃	26.2
玻璃，96％二氧化硅	19
镍铬铁合金	79
铁，球墨铸铁	63-66
铁，可锻	64
凯夫拉	19
铅	13.1
镁	16.5
钼	118
蒙乃尔合金	66
镍银	48
镍钢	76
尼龙	4.1
磷青铜	41
胶合板	0.62
聚碳酸酯纤维	2.3
聚乙烯	0.12
橡胶	0.0003
结构钢	79.3
不锈钢	77.2
铸钢	78
钢，冷轧	75
锡	18
钛2级	41
5级钛	41
钛，10％钒	42
钨丝	161
木材，道格拉斯杉木	13
锌锌	43
锌镍	76

注：

1 GPa = 10⁹ Pa = 0.145 x 10⁶ psi (lb_f/in²)

1 x 10⁶ psi = 6.9 GPa

1  摩擦（Friction）

两个相互接触并挤压的物体，当它们发生相对运动或具有相对运动趋势时，就会在接触面上产生阻碍相对运动或相对运动趋势的力，这种力叫做摩擦力。

摩擦力的计算式为：

静摩擦：静摩擦是一个物体在另一个物体表面上具有相对运动趋势时，但并没有发生相对运动时，所受到的阻碍物体相对运动趋势的力。

滑动摩擦：一物体沿着另一物体的表面运动时，在其接触面所产生的阻力。

2   某些常见材料和材料组合的摩擦系数

材料1	材料2	表面条件	– μ 静 –	– μ 滑动 –
铝	铝	清洁干燥	1.05-1.35	1.4
铝	铝	润滑和油腻	0.3
铝青铜	钢	清洁干燥	0.45
铝	软钢	清洁干燥	0.61	0.47
铝	雪	湿	0.4
铝	雪	干燥	0.35
刹车片	铸铁	清洁干燥	0.4
刹车片	铸铁（湿式）	清洁干燥	0.2
黄铜	钢	清洁干燥	0.51	0.44
黄铜	钢	润滑和油腻	0.19
黄铜	钢	蓖麻油	0.11
黄铜	铸铁	清洁干燥		0.3
黄铜	冰	清洁		0.02
黄铜	冰	清洁		0.15
砖	木	清洁干燥	0.6
青铜	钢	润滑和油腻	0.16
青铜	铸铁	清洁干燥		0.22
青铜-烧结	钢	润滑和油腻	0.13
镉	镉	清洁干燥	0.5
镉	镉	润滑和油腻	0.05
镉	铬	清洁干燥	0.41
镉	铬	润滑和油腻	0.34
镉	软钢	清洁干燥		0.46
铸铁	铸铁	清洁干燥	1.1	0.15
铸铁	铸铁	清洁干燥		0.15
铸铁	铸铁	润滑和油腻		0.07
铸铁	橡木	清洁干燥		0.49
铸铁	橡木	润滑和油腻		0.075
铸铁	软钢	清洁干燥	0.4
铸铁	软钢	清洁干燥		0.23
铸铁	软钢	润滑和油腻	0.21	0.133
汽车轮胎	沥青	清洁干燥	0.72
汽车轮胎	草	清洁干燥	0.35
碳（硬）	碳	清洁干燥	0.16
碳（硬）	碳	润滑和油腻	0.12-0.14
碳	钢	清洁干燥	0.14
碳	钢	润滑和油腻	0.11-0.14
铬	铬	清洁干燥	0.41
铬	铬	润滑和油腻	0.34
铜铅合金	钢	清洁干燥	0.22
铜	铜	清洁干燥	1.6
铜	铜	润滑和油腻	0.08
铜	铸铁	清洁干燥	1.05	0.29
铜	软钢	清洁干燥	0.53	0.36
铜	软钢	润滑和油腻		0.18
铜	软钢	油酸		0.18
铜	玻璃	清洁干燥	0.68	0.53
棉	棉	线程数	0.3
钻石	钻石	清洁干燥	0.1
钻石	钻石	润滑和油腻	0.05-0.1
钻石	金属制品	清洁干燥	0.1-0.15
钻石	金属	润滑和油腻	0.1
石榴石	钢	清洁干燥		0.39
玻璃	玻璃	清洁干燥	0.9-1.0	0.4
玻璃	玻璃	润滑和油腻	0.1-0.6	0.09-0.12
玻璃	金属	清洁干燥	0.5-0.7
玻璃	金属	润滑和油腻	0.2-0.3
玻璃	镍	清洁干燥	0.78
玻璃	镍	润滑和油腻	0.56
石墨	钢	清洁干燥	0.1
石墨	钢	润滑和油腻	0.1
石墨	石墨（真空中）	清洁干燥	0.5-0.8
石墨	石墨	清洁干燥	0.1
石墨	石墨	润滑和油腻	0.1
麻绳	木材	清洁干燥	0.5
马蹄铁	橡胶	清洁干燥	0.68
马蹄铁	具体	清洁干燥	0.58
冰	冰	清洁	0.1	0.02
冰	冰	清洁(-12°C）	0.3	0.035
冰	冰	清洁（-80 °C）	0.5	0.09
冰	木	清洁干燥	0.05
冰	钢	清洁干燥	0.03
铁	铁	清洁干燥	1
铁	铁	润滑和油腻	0.15-0.20
铅	铸铁	清洁干燥		0.43
皮革	橡木	与谷物平行	0.61	0.52
皮革	金属	清洁干燥	0.4
皮革	金属	润滑和油腻	0.2
皮革	木	清洁干燥	0.3-0.4
皮革	清洁金属	清洁干燥	0.6
皮革	铸铁	清洁干燥	0.6	0.56
皮革纤维	铸铁	清洁干燥	0.31
皮革纤维	铝	清洁干燥	0.3
镁	镁	清洁干燥	0.6
镁	镁	润滑和油腻	0.08
镁	钢	清洁干燥		0.42
镁	铸铁	清洁干燥		0.25
石工	砖	清洁干燥	0.6-0.7
云母	云母	刚劈开	1
镍	镍	清洁干燥	0.7-1.1	0.53
镍	镍	润滑和油腻	0.28	0.12
镍	软钢	清洁干燥		0.64
镍	软钢	润滑和油腻		0.178
尼龙	尼龙	清洁干燥	0.15-0.25
尼龙	钢	清洁干燥	0.4
尼龙	雪	湿0 °C	0.4
尼龙	雪	干燥-10 ° C	0.3
橡木	橡木（平行纹理）	清洁干燥	0.62	0.48
橡木	橡木（杂粮）	清洁干燥	0.54	0.32
橡木	橡木（杂粮）	润滑和油腻		0.072
纸	铸铁	清洁干燥	0.2
磷青铜	钢	清洁干燥	0.35
铂	铂	清洁干燥	1.2
铂	铂	润滑和油腻	0.25
Plexiglas	Plexiglas	清洁干燥	0.8
Plexiglas	Plexiglas	润滑和油腻	0.8
Plexiglas	钢	清洁干燥	0.4-0.5
Plexiglas	钢	润滑和油腻	0.4-0.5
聚苯乙烯	聚苯乙烯	清洁干燥	0.5
聚苯乙烯	聚苯乙烯	润滑和油腻	0.5
聚苯乙烯	钢	清洁干燥	0.3-0.35
聚苯乙烯	钢	润滑和油腻	0.3-0.35
聚乙烯	聚乙烯	清洁干燥	0.2
聚乙烯	钢	清洁干燥	0.2
聚乙烯	钢	润滑和油腻	0.2
橡胶	橡胶	清洁干燥	1.16
橡胶	纸板	清洁干燥	0.5-0.8
橡胶	干沥青	清洁干燥	0.9	0.5-0.8
橡胶	湿沥青	清洁干燥		0.25-0.75
橡胶	干混凝土	清洁干燥		0.6-0.85
橡胶	湿混凝土	清洁干燥		0.45-0.75
丝	丝	清洁	0.25
银	银	清洁干燥	1.4
银	银	润滑和油腻	0.55
蓝宝石	蓝宝石	清洁干燥	0.2
蓝宝石	蓝宝石	润滑和油腻	0.2
银	银	清洁干燥	1.4
银	银	润滑和油腻	0.55
皮肤	金属制品	清洁干燥	0.8-1.0
钢	钢	清洁干燥	0.5-0.8	0.42
钢	钢	润滑和油腻	0.16
钢	钢	蓖麻油	0.15	0.081
钢	钢	硬脂酸		0.15
钢	钢	轻质矿物油	0.23
钢	钢	猪油	0.11	0.084
钢	钢	石墨		0.058
钢	石墨	清洁干燥	0.21
秸秆纤维	铸铁	清洁干燥	0.26
秸秆纤维	铝	清洁干燥	0.27
焦油纤维	铸铁	清洁干燥	0.15
焦油纤维	铝	清洁干燥	0.18
聚四氟乙烯（PTFE）（铁氟龙）	聚四氟乙烯（PTFE）	清洁干燥	0.04	0.04
聚四氟乙烯（PTFE）	聚四氟乙烯（PTFE）	润滑和油腻	0.04
聚四氟乙烯（PTFE）	钢	清洁干燥	0.05-0.2
聚四氟乙烯（PTFE）	雪	湿 0 °C	0.05
聚四氟乙烯（PTFE）	雪	干燥0 °Ç	0.02
碳化钨	钢	清洁干燥	0.4-0.6
碳化钨	钢	润滑和油腻	0.1-0.2
碳化钨	碳化钨	清洁干燥	0.2-0.25
碳化钨	碳化钨	润滑和油腻	0.12
碳化钨	铜	清洁干燥	0.35
碳化钨	铁	清洁干燥	0.8
锡	铸铁	清洁干燥		0.32
轮胎干	干路	清洁干燥	1个
湿轮胎	湿路	清洁干燥	0.2
蜡，滑雪	雪	湿0 °C	0.1
蜡，滑雪	雪	干燥0 °Ç	0.04
蜡，滑雪	雪	干燥-10 °C	0.2
木	清洁木材	清洁干燥	0.25-0.5
木	湿木	清洁干燥	0.2
木	清洁金属	清洁干燥	0.2-0.6
木	湿金属	清洁干燥	0.2
木	结石	清洁干燥	0.2-0.4
木	具体	清洁干燥	0.62
木	砖	清洁干燥	0.6
木材打蜡	湿雪	清洁干燥	0.14	0.1
木材打蜡	干燥的雪	清洁干燥		0.04
锌锌	铸铁	清洁干燥	0.85	0.21
锌锌	锌锌	清洁干燥	0.6
锌锌	锌锌	润滑和油腻	0.04

1 润滑良好的轴承类型的机器元件的典型效率

类型	效率
普通轴承	95-98％
滚子轴承	98％
球轴承	99％
切齿正齿轮，包括轴承	99％
带有齿的锥齿轮，包括轴承	98％
皮带	96-98％
高功率静音传输链	97-99％
滚子链	95-97％
自行车链条导轨装置	87-97％
自行车变速器	86-95％

表 1

1 盘式制动器-压力和扭矩

盘式制动器又称为碟式制动器，制动盘用合金钢制造并固定在车轮上，随车轮转动。

图 1

具有两个刹车片的盘式制动器的扭矩可以表示为

T = 2 μ F r

式 1

其中：

• T =制动扭矩（Nm）

• μ= 摩擦系数

• F =每个垫上的力（N）

• r =平均半径（从中心轮到刹车片中心）（m）

刹车片上承受的的压力表示为：

p = F / A 

式 2

其中：

• p = 压力 (Pa)

• A = 刹车片承压面积 (m²)

1        热膨胀-应力和力

图 1

温度变化引起的线性膨胀可表示为:

dl = α l₀ dt 

式 1

其中：

• dl =伸长量（m）

• α= 温度膨胀系数（m / mK）某一方向上的长度的变化和它在20℃（即标准实验室环境）时的长度的比值

• l₀=初始长度（m）

• dt =温差（°C）

若热膨胀无限制将产生的应变或变形可以表示为

ε= dl / l₀

式 2

其中：

• ε=应变

由此产生的应力可以表示为：

σ = Eε

式 3

其中：

• σ= 应力（Pa（N / m 2），psi）

• ε=应变

因此两端被限制的圆柱所产生的轴向力可由下式计算：

F = σ_dt A 

   = E α dt A 

式 4

其中：

• F = 轴向力 (N)

• A = 圆柱截面面积 (m²)

2 算例

图一中圆柱铸铁横截面面积为1000 mm², 热膨胀系数为12.2×10^-6 m/m·K，初始长度l₀为300mm，杨氏模量为155GPa，温差为20 °C。

由此产生的轴向力可以计算为：

dl = (12.2×10^-12 m/mK) (300 mm) (20 ^oC)

    = 7.32×10^-11 m

ε= dl / l₀

  =(7.32×10^-11 m)/ (300mm)

  =2.44×10^-10

σ= Eε=(155 GPa) · 2.44×10^-10=37.8 Pa (N/m²)

                                F= σ_dt A =（37.8 Pa）×（1000mm²) = 0.03782 N

1 风速和风荷载

当移动的空气（风）被表面阻止时，风的动能转化为压力。

其作用于表面的压力计算式为：

F_w = p_d A

     = 1/2 ρ v² A 

式 1

其中：

• F_W = 风力（N）
• A =表面积（m²）
• p_d= 动压（Pa）
• ρ= 空气密度（kg / m³）–1个大气压下，25°C的空气密度为1.2 Kg/m³
• v =风速（m / s）

注意-实际上，作用在物体上的风力会由于阻力，表面形状，空气湍流等等影响而产生更复杂的力。上式可用作简单风压力的计算。

图 1

风速 (m/s)	风压 (Pa)
1	0.6
2	2.4
3	5.4
4	9.6
5	15
6	22
7	29
8	38
9	49
10	60
11	73
12	86
13	101
14	118
15	135
16	154
17	173
18	194
19	217
20	240
21	265
22	290
23	317
24	346
25	375
26	406
27	437
28	470
29	505
30	540
31	577
32	614
33	653
34	694
35	735
36	778
37	821
38	866
39	913
40	960
41	1009
42	1058
43	1109
44	1162
45	1215
46	1270
47	1325
48	1382
49	1441
50	1500

2 算例

风速为35 m / s的飓风作用在1 m²的墙壁上。

其风力可以计算为：

F _w = 1/2 ρv ² A  

    = 1/2（1.2 kg / m ³）（35 m / s）²（1 m ²）

    = 735 N

   =75 Kg

1 螺纹千斤顶

螺纹千斤顶是一种常见的千斤顶。

图 1

其原理是利用螺旋副传动的力放大效应实现架高重物。

图 2

忽略摩擦时，千斤顶的手推力可以表示为：

F = (Q p) / (2πR)

式 1

其中：

• F =手臂或手柄末端的力量（N）
• Q = 需要顶起的重量或负载（N）
• p = 螺距-一圈的距离或线距（m）
• R = 杠杆臂半径（m）

作用在螺纹上的扭矩可以计算为

T = F R 

式 2

其中：

• T = 扭矩 (Nm)
• R = 杠杆臂半径（m）

2 算例

如果螺旋千斤顶的负载为2t（2000 Kg），则杠杆臂为30 cm，螺距等于3mm，所需扭转力可以估算为：

F = ((2000 Kg) (3 mm)) / (2 π (30 cm))

    = 31.2 N

扭矩：

T = (31.2 N) (30 cm)

    = 9.36 N m 

1  刚度 （Stiffness）

刚度是指零件在载荷作用下抵抗弹性变形的能力。

定义为施力与所产生变形量的比值，表示材料或结构抵抗变形的能力。

计算公式为：

K=P/?

式 1

其中：

• K = 刚度 （N/m）
• P = 载荷 （N）
• ? = 变形量 （m）

2  弹性模量与刚度的区别

弹性模量（Modulus）是材料组成的性质；刚度（Stiffness）是结构的性质。即模量是材料的本身的性质；刚度是固体的外延性质，它取决于材料，形状及边界条件。结构刚度在许多工程应用当中非常重要。

对于一个受压或受拉的物体，其轴向刚度为：

K=AE/L

式 2

其中：

• A= 横截面面积 （m²）；
• E= 为拉伸弹性模量-杨氏模量 （MPa）；
• L= 为物体的长度 （m）

对于一个受扭的物体，其扭转刚度为：

K=ML/θ

式 3

其中：

• M= 作用的扭矩（N·m）；
• L= 扭矩作用处到固定端的距离（m）；
• θ= 扭转角（°）

1  回弹硬度（Rebound Hardness）

回弹硬度也称里氏回弹硬度测试（LRHT）是测试金属硬度的四种最常用方法之一。这种便携式方法主要用于测试足够大的工件（主要是1 kg以上）。主要用于金属材料。回弹硬度又称为冲撞硬度和马尔特氏硬度，它测量的是一个带金刚石触头的重锤从一定高度落向被测物质以后弹回的高度。

 

方法是用特制的小锤从一定高度自由下落冲击被测材料的试样，并以试样在冲击过程中储存（继而释放）应变能的多少（通过小锤的回跳高度测定）确定材料的硬度。

 

里氏硬度优点是对产品表面损伤很轻，有时可作为无损检测；对各个方向，窄小空间及特殊部位硬度测试具有独特性。

 

详细测试方法，请参阅标准DIN 50156、ASTM A956、ISO/DIS 16859。

 

2  回弹硬度计

1 压入硬度

压入硬度（Indentation hardness）用来反映一种物质抵抗形变的能力。在压入硬度测试里，被测物质经过数次检测直到表面产生压痕。而压入硬度测试可以在宏观或者微观的条件下进行。

压入硬度主要应用于工程学和冶金术，它从多方面描述物质的抗形变性质，如抗永久形变和特别的抗弹性形变。通常测量压入硬度是通过在被测物质上加载一个特定形状的压头然后测量其产生的形变量。

有很多其他压入硬度的定义，其中常见的几种有：

• 布氏硬度 (HB)
• 杨卡木材硬度等级
• 努氏硬度 (HK) 或称微硬度测试，用来测试小面积物质
• 迈氏硬度
• 洛氏硬度测试 (HR)，主要用于美国
• 肖氏硬度 用于聚合体强度
• 维氏硬度 (HV)，有最大的定义范围
• 巴氏硬度，用于合成材料，范围从0到100

三种最常用压入硬度介绍：

1.1 布氏硬度

布氏硬度试验是压入硬度试验之一种，其测量值用HB或BHN表示。布氏硬度试验一般采用直径10毫米的球形钢压头，用一定的负荷（试验力）压入被测材料表面。常见的试验力可高达3,000 Kg（29 KN）；对于软的材料则可用较小的负荷。如果试验材料很硬，则以碳化钨球压头代替钢压头。保持负荷一定时间后，卸除试验力，测量材料表面留下的压痕之直径。具体实验请参考国家标准GB／T231或国际标准ISO 6506。

布氏硬度值的计算公式为：

其中：

• P = 载荷（N）
• D = 压头直径（mm）
• d = 压痕直径（mm）

常见材料布氏硬度：

1.2 洛氏硬度

洛氏硬度（英语：Rockwell hardness test），压入硬度的一种。洛氏硬度是以压痕塑性变形深度来确定硬度值的指标，以0.002毫米作为一个硬度单位。在洛氏硬度试验中采用不同的压头和不同的试验力，会产生不同的组合，对应于洛氏硬度不同的标尺。常用的有3个标尺（HRA、HRB、HRC），其应用涵盖了几乎所有常用的金属材料。洛氏硬度试验方法广泛应用于生产制造、科学研究的各个领域。

1.2.1   硬度标尺

三种压头

• 金刚石锥压入器
• 钢球压头，直径1.588毫米（1/16″）或3.175毫米
• 硬质合金球压头

三种试验载荷

• 60 Kg
• 100 Kg
• 150 Kg

HRA 60kg载荷金刚石锥压入器；

HRB 100kg载荷1/16″直径钢球压头；

HRC 150kg载荷金刚石锥压入器；

最常用标尺是HRC、HRB和HRF，其中HRC标尺用于测试淬火钢、回火钢、调质钢和部分不锈钢。这是金属加工行业应用最多的硬度试验方法。

HRB标尺用于测试各种退火钢、正火钢、软钢、部分不锈钢及较硬的铜合金。

HRF标尺用于测试纯铜、较软的铜合金和硬铝合金。

HRA标尺尽管也可用于大多数黑色金属，但是实际应用上一般只限于测试硬质合金和薄硬钢带材料。

• 表面洛氏硬度试验采用三种试验力，两种压头，它们有6种组合，对应于表面洛氏硬度的6个标尺。表面洛氏硬度试验是对洛氏硬度试验的一种补充，在采用洛氏硬度试验时，当遇到材料较薄，试样较小，表面硬化层较浅或测试表面镀覆层时，就应改用表面洛氏硬度试验。这时采用与洛氏硬度试验相同的压头，采用只有洛氏硬度试验几分之一大小的试验力，就可以在上述试样上得到有效的硬度试验结果。表面洛氏硬度的N标尺适用于类似洛氏硬度的HRC、HRA和HRD测试的材料；T标尺适用于类似洛氏硬度的HRB、HRF和HRG测试的材料。

标尺列表

详细测试方法，请查阅国家标准GB/T230或国际标准ISO 6508，或美标ASTM E18。

1.3 维氏硬度

维氏硬度（英语：Vickers hardness test），压入硬度试验的一种，其测量值用HV表示。维氏硬度试验最初于20世纪20年代初被提出，比起其他硬度试验其优点有：硬度值与压头大小、负荷值无关；无需根据材料软硬变换压头；正方形的压痕轮廓边缘清晰，便于测量。维氏硬度被应用于所有金属，并是应用最广泛的硬度标准之一。只要被测材料质地均匀，维氏硬度试验可以用低负荷和小压痕得到可靠的硬度值，这样能减少材料破坏，或用于薄小的试验材料。这一点上维氏硬度要优于布氏硬度。在硬度不高（硬度值400HV以下）的同一均匀材料上，维氏和布氏硬度试验得出的数值近似。

• 测试方法：维氏硬度试验使用正四棱锥形的金刚石压头，其相对面夹角为136°。由于其硬度极高，金刚石压头可以用于压入几乎所有材料，而且棱锥的形状使得压痕和压头本身的大小无关。将压头用一定的负荷（试验力）压入被测材料表面。保持负荷一定时间后，卸除负荷，测量材料表面的方形压痕之对角线长度。对相互垂直的二对角线长度（l₁和l₂）取其平均值。

图 1

上图左为压痕在材料表面的投影，l₁和l₂为压痕对角线长；右为金刚石压头的侧面观，其相对面夹角为136°。

其量纲为N/mm²，计算公式为：

式 1

其中：

• F = 负荷（N）
• S = 压痕表面积（mm²）
• α = 压头相对面夹角=136°
• d = 平均压痕对角线长度（m）
• g = 标准重力加速度（9.80665 m/s²）

例如440HV30中，440是维氏硬度值，30指的是测量所用的负荷值（单位：kg）

详细测试方法，请查阅国家标准GB/T4340或国际标准ISO 6507。