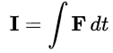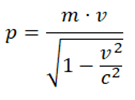1  皮带传动的功率和效率的计算方法

以上图为例，从动轮A上的扭矩可以用下式计算：

T = (F₂ – F₁) r_a

其中：

• T = 扭矩 (Nm)
• F = 力 (N)
• r = 皮带轮半径 (m)

1.1  皮带传动有效功率的计算公式：

P = T ω_a = (F₂ – F₁) r_a ω_a

其中：

• P = 传递的有效功率(w，瓦特)
• ω_a = 角速度 (rad/s，弧度/秒)

1.2  皮带传动效率的计算公式：

η = P_A/P_B= (F₂ – F₁) r_a ω_a/P_B

其中：

• η = 皮带传动效率（%）
• P_A = 传递的有效功率(w，瓦特)
• P_B = 来自电机或发动机的输出功率(w，瓦特)

倾斜转弯是指车辆通常向转弯内侧倾斜或倾斜的转弯或方向变化。对于绕圆运动的车辆（例如火车或弯道上的汽车），车辆上的车轮会向着圆心产生向心加速度。道路或轨道会受到离心推力，试图使道路或轨道向外移动。

1  汽车倾角转弯

如上图所示转弯时路面提供给汽车的向心力可以表示为：

N sinθ=mv²/r

汽车重力可以表示为：

N cosθ=mg

• Θ = 倾斜角 (°)
• v = 速度 (m/s)
• r = 转弯半径 (m)
• g = 重力加速度 (9.81 m/s²) 

联立上面两个式子可得：

tanθ = v²/ (r g)

将上式变化一下，我们很容易得出当倾角θ确定时，汽车行驶允许的最大速度。

v=(r g tanθ)^1/2

注：以上均为理想条件下-即不考虑汽车轮胎与地面的摩擦力

2  飞机的倾角转弯

飞机飞行时也同样需要分析其倾角转弯。由于空气在机翼上的作用力，升力与机翼成直角。当飞机倾斜时，飞行员获得的升力超过了水平飞行所需的升力。升力的垂直分量平衡了飞机的重量，水平分量使飞机加速。倾斜角由θ给出。计算飞机倾角转弯时候，可以使用汽车倾角转弯的相同方式。

1  谐波振荡器

可以将简单的谐波运动用作各种运动（例如弹簧的振动）的数学模型。

简单谐波振荡器的时间周期可以表示为：

T = 2 π (m / k)^1/2

• T = 时间 (s)
• m = 质量 (kg)
• k = 弹簧的强度系数 (N/m)

2  算例-简单谐波振荡器的震荡周期

500 kg的质量连接到弹簧常数为16000 N / m的弹簧上。震荡周期可以计算为：

T = 2π（（500kg）/（16000 N / m））^1/2

  = 1.1s

1  胡克定律

胡克定律/虎克定律(Hooke’s law)，是力学弹性理论中的一条基本定律，内容：固体材料受力后，应力与应变(单位变形量)成线性关系，满足此定律的材料：线弹性/胡克型(Hookean)。从物理的角度看，胡克定律源于多数固体(或孤立分子)内部的原子在无外载作用下处于稳定平衡的状态。

胡克定律应用的一个常见例子是弹簧。在弹性限度内，弹簧的弹力F和弹簧的长度变化量s成线性关系，拉伸或压缩弹簧所需的力可以用胡克定律表示为

F = – k s

• F = 力 (N)
• k  = 弹簧强度系数 (N/m)
• s = 弹簧长度变化 (m)

2  胡克定律的广义变化

在胡克定律的广义变化中，它指出弹性物体或材料的应变/变形与施加于其上的应力成比例。它可以用数学表示为

σ= Eε

其中：

• σ=应力（Pa）
• E =杨氏弹性模量（Pa）
• ε=应变（m / m）

胡克定律仅适用于特定加载条件下的部分材料。钢材在多数工程应用中都可视为线弹性材料，在弹性范围内（即应力低于屈服强度时）胡克定律都适用。另外一些材料（如铝材）则只在弹性范围内的一部分区域行为符合胡克定律。对于这些材料需要定义一个应力线性极限，在应力低于该极限时线性描述带来的误差可以忽略不计。

还有一些材料在任何情况下都不满足胡克定律（如橡胶），这种材料称为“非胡克型”（neo-hookean）材料。橡胶的刚度不仅和应力水平相关，还对温度和加载速率十分敏感。

胡克定律在磅秤制造、应力分析和材料模拟等方面有广泛的应用。

1  飞轮简介

飞轮（flywheel）是指转动惯量很大的零部件，可用于消除能量波动，并使间歇运行的能量流更均匀。能量以动能的形式存储在飞轮中。内燃机飞轮是最为常见的飞轮应用，一个活塞式的四冲程发动机，除了做功行程，其它的三个进气、压缩和排气行程都要靠飞轮储存的能量来维持旋转。

2 飞轮中存储的动能

E_f = 1/2 I ω²

• E_f = 飞轮种存储的动能 (Nm, J)
• I = 飞轮的转动惯量 (kg m²)
• ω = 飞轮的角速度 (rad/s)

角速度的角度-弧度转换：

1 rad = 360° / 2 π =~ 57.29578°

1 rad/s = 9.55 转/min (rpm) = 0.159 转/s (rps)

• rpm=round per minute 即：转/分
• rps= round per second 即：转/秒

转动惯量I可以表示为:

I = k m r²

其中：

• k = 转动惯量系数–取决于飞轮的形状
• m = 飞轮质量 (kg)
• r = 飞轮半径 (m)

几种常见飞轮的惯性常数

• 轮辋像自行车轮胎一样装在轮辋上-k = 1
• 厚度均匀的扁平实心圆盘-k = 0.606
• 带中心孔的平盘-k =〜0.3
• 实心球-k = 2/5
• 薄边-k = 0.5
• 径向杆-k = 1/3
• 圆形刷子-k = 1/3
• 薄壁空心球-k = 2/3
• 细矩形杆-k = 1/2

3  算例示例-旋转自行车车轮中的能量

典型的26英寸自行车轮辋的直径为559mm，轮胎外径约为665mm（26.2英寸）。为了方便计算，将车轮的半径-r-近似为

r =（（665mm）+（559mm）/ 2）/ 2

  = 306 mm

  = 0.306 m

车轮的重量为2.3 kg，惯性常数为k = 1。

可以计算出车轮的惯性矩

I =（1）（2.3 kg）（0.306 m）² 

   = 0.22 kg m²

自行车的速度为25 km / h（6.94 m / s）。车轮圆周速度（rps即转/ s）-n _rps- 可以计算为

n _rps =（6.94 m / s）/（2π（0.665 m）/ 2）

     = 3.32转/ s

车轮的角速度可以计算为

ω=（3.32转/s）（2π rad/转）

   = 20.9 rad/ s

然后可以计算出旋转的自行车车轮的动能为

E _f = 0.5（0.22 kg m ²）（20.9 rad / s）²     

  = 47.9 焦耳

1        曲柄连杆机构的计算

曲柄连杆机构将旋转运动转换为往复运动-反之亦然。

图 1

杆端头的位置可以表示为：

s = r (1 – cos φ) + (λ / 2) r sin²φ

式 1

其中：              s = 连杆位置 (m)

r = 曲柄半径 (m)

φ = ω t

   = 2 π n_s t

式 2

其中：ω          = 曲柄角速度 (rad/s)

t        = 时间 (s)

n_s      = 曲柄转速 (转/s)

λ = r / l

式 3

其中：l =杆长（m）

λ = 连杆比

连杆端头速度：

v = ω r sin φ (1 + λ cos φ)

式 4

其中：v = 连杆沿导轨的速度 (m/s)

连杆端头加速度：

a = ω2 r (cos φ + λ cos 2φ) 

式 5

其中：a = 连杆加速度 (m/s²)

1  摩擦（Friction）

两个相互接触并挤压的物体，当它们发生相对运动或具有相对运动趋势时，就会在接触面上产生阻碍相对运动或相对运动趋势的力，这种力叫做摩擦力。

摩擦力的计算式为：

静摩擦：静摩擦是一个物体在另一个物体表面上具有相对运动趋势时，但并没有发生相对运动时，所受到的阻碍物体相对运动趋势的力。

滑动摩擦：一物体沿着另一物体的表面运动时，在其接触面所产生的阻力。

2   某些常见材料和材料组合的摩擦系数

材料1	材料2	表面条件	– μ 静 –	– μ 滑动 –
铝	铝	清洁干燥	1.05-1.35	1.4
铝	铝	润滑和油腻	0.3
铝青铜	钢	清洁干燥	0.45
铝	软钢	清洁干燥	0.61	0.47
铝	雪	湿	0.4
铝	雪	干燥	0.35
刹车片	铸铁	清洁干燥	0.4
刹车片	铸铁（湿式）	清洁干燥	0.2
黄铜	钢	清洁干燥	0.51	0.44
黄铜	钢	润滑和油腻	0.19
黄铜	钢	蓖麻油	0.11
黄铜	铸铁	清洁干燥		0.3
黄铜	冰	清洁		0.02
黄铜	冰	清洁		0.15
砖	木	清洁干燥	0.6
青铜	钢	润滑和油腻	0.16
青铜	铸铁	清洁干燥		0.22
青铜-烧结	钢	润滑和油腻	0.13
镉	镉	清洁干燥	0.5
镉	镉	润滑和油腻	0.05
镉	铬	清洁干燥	0.41
镉	铬	润滑和油腻	0.34
镉	软钢	清洁干燥		0.46
铸铁	铸铁	清洁干燥	1.1	0.15
铸铁	铸铁	清洁干燥		0.15
铸铁	铸铁	润滑和油腻		0.07
铸铁	橡木	清洁干燥		0.49
铸铁	橡木	润滑和油腻		0.075
铸铁	软钢	清洁干燥	0.4
铸铁	软钢	清洁干燥		0.23
铸铁	软钢	润滑和油腻	0.21	0.133
汽车轮胎	沥青	清洁干燥	0.72
汽车轮胎	草	清洁干燥	0.35
碳（硬）	碳	清洁干燥	0.16
碳（硬）	碳	润滑和油腻	0.12-0.14
碳	钢	清洁干燥	0.14
碳	钢	润滑和油腻	0.11-0.14
铬	铬	清洁干燥	0.41
铬	铬	润滑和油腻	0.34
铜铅合金	钢	清洁干燥	0.22
铜	铜	清洁干燥	1.6
铜	铜	润滑和油腻	0.08
铜	铸铁	清洁干燥	1.05	0.29
铜	软钢	清洁干燥	0.53	0.36
铜	软钢	润滑和油腻		0.18
铜	软钢	油酸		0.18
铜	玻璃	清洁干燥	0.68	0.53
棉	棉	线程数	0.3
钻石	钻石	清洁干燥	0.1
钻石	钻石	润滑和油腻	0.05-0.1
钻石	金属制品	清洁干燥	0.1-0.15
钻石	金属	润滑和油腻	0.1
石榴石	钢	清洁干燥		0.39
玻璃	玻璃	清洁干燥	0.9-1.0	0.4
玻璃	玻璃	润滑和油腻	0.1-0.6	0.09-0.12
玻璃	金属	清洁干燥	0.5-0.7
玻璃	金属	润滑和油腻	0.2-0.3
玻璃	镍	清洁干燥	0.78
玻璃	镍	润滑和油腻	0.56
石墨	钢	清洁干燥	0.1
石墨	钢	润滑和油腻	0.1
石墨	石墨（真空中）	清洁干燥	0.5-0.8
石墨	石墨	清洁干燥	0.1
石墨	石墨	润滑和油腻	0.1
麻绳	木材	清洁干燥	0.5
马蹄铁	橡胶	清洁干燥	0.68
马蹄铁	具体	清洁干燥	0.58
冰	冰	清洁	0.1	0.02
冰	冰	清洁(-12°C）	0.3	0.035
冰	冰	清洁（-80 °C）	0.5	0.09
冰	木	清洁干燥	0.05
冰	钢	清洁干燥	0.03
铁	铁	清洁干燥	1
铁	铁	润滑和油腻	0.15-0.20
铅	铸铁	清洁干燥		0.43
皮革	橡木	与谷物平行	0.61	0.52
皮革	金属	清洁干燥	0.4
皮革	金属	润滑和油腻	0.2
皮革	木	清洁干燥	0.3-0.4
皮革	清洁金属	清洁干燥	0.6
皮革	铸铁	清洁干燥	0.6	0.56
皮革纤维	铸铁	清洁干燥	0.31
皮革纤维	铝	清洁干燥	0.3
镁	镁	清洁干燥	0.6
镁	镁	润滑和油腻	0.08
镁	钢	清洁干燥		0.42
镁	铸铁	清洁干燥		0.25
石工	砖	清洁干燥	0.6-0.7
云母	云母	刚劈开	1
镍	镍	清洁干燥	0.7-1.1	0.53
镍	镍	润滑和油腻	0.28	0.12
镍	软钢	清洁干燥		0.64
镍	软钢	润滑和油腻		0.178
尼龙	尼龙	清洁干燥	0.15-0.25
尼龙	钢	清洁干燥	0.4
尼龙	雪	湿0 °C	0.4
尼龙	雪	干燥-10 ° C	0.3
橡木	橡木（平行纹理）	清洁干燥	0.62	0.48
橡木	橡木（杂粮）	清洁干燥	0.54	0.32
橡木	橡木（杂粮）	润滑和油腻		0.072
纸	铸铁	清洁干燥	0.2
磷青铜	钢	清洁干燥	0.35
铂	铂	清洁干燥	1.2
铂	铂	润滑和油腻	0.25
Plexiglas	Plexiglas	清洁干燥	0.8
Plexiglas	Plexiglas	润滑和油腻	0.8
Plexiglas	钢	清洁干燥	0.4-0.5
Plexiglas	钢	润滑和油腻	0.4-0.5
聚苯乙烯	聚苯乙烯	清洁干燥	0.5
聚苯乙烯	聚苯乙烯	润滑和油腻	0.5
聚苯乙烯	钢	清洁干燥	0.3-0.35
聚苯乙烯	钢	润滑和油腻	0.3-0.35
聚乙烯	聚乙烯	清洁干燥	0.2
聚乙烯	钢	清洁干燥	0.2
聚乙烯	钢	润滑和油腻	0.2
橡胶	橡胶	清洁干燥	1.16
橡胶	纸板	清洁干燥	0.5-0.8
橡胶	干沥青	清洁干燥	0.9	0.5-0.8
橡胶	湿沥青	清洁干燥		0.25-0.75
橡胶	干混凝土	清洁干燥		0.6-0.85
橡胶	湿混凝土	清洁干燥		0.45-0.75
丝	丝	清洁	0.25
银	银	清洁干燥	1.4
银	银	润滑和油腻	0.55
蓝宝石	蓝宝石	清洁干燥	0.2
蓝宝石	蓝宝石	润滑和油腻	0.2
银	银	清洁干燥	1.4
银	银	润滑和油腻	0.55
皮肤	金属制品	清洁干燥	0.8-1.0
钢	钢	清洁干燥	0.5-0.8	0.42
钢	钢	润滑和油腻	0.16
钢	钢	蓖麻油	0.15	0.081
钢	钢	硬脂酸		0.15
钢	钢	轻质矿物油	0.23
钢	钢	猪油	0.11	0.084
钢	钢	石墨		0.058
钢	石墨	清洁干燥	0.21
秸秆纤维	铸铁	清洁干燥	0.26
秸秆纤维	铝	清洁干燥	0.27
焦油纤维	铸铁	清洁干燥	0.15
焦油纤维	铝	清洁干燥	0.18
聚四氟乙烯（PTFE）（铁氟龙）	聚四氟乙烯（PTFE）	清洁干燥	0.04	0.04
聚四氟乙烯（PTFE）	聚四氟乙烯（PTFE）	润滑和油腻	0.04
聚四氟乙烯（PTFE）	钢	清洁干燥	0.05-0.2
聚四氟乙烯（PTFE）	雪	湿 0 °C	0.05
聚四氟乙烯（PTFE）	雪	干燥0 °Ç	0.02
碳化钨	钢	清洁干燥	0.4-0.6
碳化钨	钢	润滑和油腻	0.1-0.2
碳化钨	碳化钨	清洁干燥	0.2-0.25
碳化钨	碳化钨	润滑和油腻	0.12
碳化钨	铜	清洁干燥	0.35
碳化钨	铁	清洁干燥	0.8
锡	铸铁	清洁干燥		0.32
轮胎干	干路	清洁干燥	1个
湿轮胎	湿路	清洁干燥	0.2
蜡，滑雪	雪	湿0 °C	0.1
蜡，滑雪	雪	干燥0 °Ç	0.04
蜡，滑雪	雪	干燥-10 °C	0.2
木	清洁木材	清洁干燥	0.25-0.5
木	湿木	清洁干燥	0.2
木	清洁金属	清洁干燥	0.2-0.6
木	湿金属	清洁干燥	0.2
木	结石	清洁干燥	0.2-0.4
木	具体	清洁干燥	0.62
木	砖	清洁干燥	0.6
木材打蜡	湿雪	清洁干燥	0.14	0.1
木材打蜡	干燥的雪	清洁干燥		0.04
锌锌	铸铁	清洁干燥	0.85	0.21
锌锌	锌锌	清洁干燥	0.6
锌锌	锌锌	润滑和油腻	0.04

1 风速和风荷载

当移动的空气（风）被表面阻止时，风的动能转化为压力。

其作用于表面的压力计算式为：

F_w = p_d A

     = 1/2 ρ v² A 

式 1

其中：

• F_W = 风力（N）
• A =表面积（m²）
• p_d= 动压（Pa）
• ρ= 空气密度（kg / m³）–1个大气压下，25°C的空气密度为1.2 Kg/m³
• v =风速（m / s）

注意-实际上，作用在物体上的风力会由于阻力，表面形状，空气湍流等等影响而产生更复杂的力。上式可用作简单风压力的计算。

图 1

风速 (m/s)	风压 (Pa)
1	0.6
2	2.4
3	5.4
4	9.6
5	15
6	22
7	29
8	38
9	49
10	60
11	73
12	86
13	101
14	118
15	135
16	154
17	173
18	194
19	217
20	240
21	265
22	290
23	317
24	346
25	375
26	406
27	437
28	470
29	505
30	540
31	577
32	614
33	653
34	694
35	735
36	778
37	821
38	866
39	913
40	960
41	1009
42	1058
43	1109
44	1162
45	1215
46	1270
47	1325
48	1382
49	1441
50	1500

2 算例

风速为35 m / s的飓风作用在1 m²的墙壁上。

其风力可以计算为：

F _w = 1/2 ρv ² A  

    = 1/2（1.2 kg / m ³）（35 m / s）²（1 m ²）

    = 735 N

   =75 Kg

1 螺纹千斤顶

螺纹千斤顶是一种常见的千斤顶。

图 1

其原理是利用螺旋副传动的力放大效应实现架高重物。

图 2

忽略摩擦时，千斤顶的手推力可以表示为：

F = (Q p) / (2πR)

式 1

其中：

• F =手臂或手柄末端的力量（N）
• Q = 需要顶起的重量或负载（N）
• p = 螺距-一圈的距离或线距（m）
• R = 杠杆臂半径（m）

作用在螺纹上的扭矩可以计算为

T = F R 

式 2

其中：

• T = 扭矩 (Nm)
• R = 杠杆臂半径（m）

2 算例

如果螺旋千斤顶的负载为2t（2000 Kg），则杠杆臂为30 cm，螺距等于3mm，所需扭转力可以估算为：

F = ((2000 Kg) (3 mm)) / (2 π (30 cm))

    = 31.2 N

扭矩：

T = (31.2 N) (30 cm)

    = 9.36 N m 

1 冲量定义

冲量是作用在物体上的力在时间上的累积。冲量的量纲和单位都与动量一样，即：（kg·m/s或N·s） 表现的是一个随时间改变的力对一个物体的冲量指这个力的作用对时间的积累效果。

即力对时间的积分：

式 1

其中：

• I是冲量（也记作J）
• F是作用的力 （N）
• t是时间 （s）

2 算例

1000 N的力在10秒内作用在质量为 1000 kg的物体上。

图 1

冲量变化计算如下：

I = (1000 N) (10 s)

  = 10000 (N·s, kg·m/s)

1 动量

1.1 动量定义

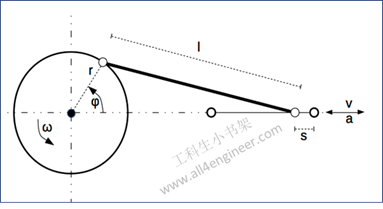
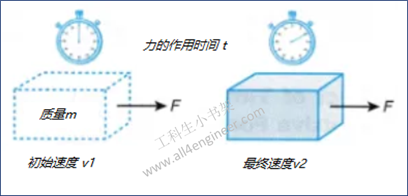
在经典力学里，动量（momentum）被量化为物体的质量和速度的乘积。直观表现为一个物体的动量指的是这个物体在它运动方向上保持运动的趋势。动量在国际单位制中的单位为kg·m/s。动量是个矢量。

p=m·v

式 1

式 2

其中：

• P=动量
• m= 质量 （Kg）-静止质量
• v= 速度（m/s）
• c= 光速 （299792458m/s）

注：一般情况用式1

在给定方向上碰撞之前的两个或多个物体的总动量等于在相同方向上碰撞之后的物体的总动量，可以表示为：

M _L = m ₁ v ₁ + m ₂ v ₂ + .. + m _n v _n

        = m ₁ u ₁ + m ₂ u ₂ + .. + m _n u _n   

• v =碰撞前物体的速度（m / s）
• u =碰撞后物体的速度（m / s）

1.2 动量守恒定律

动量是一个守恒量，即在一个封闭系统内动量的总和不可改变。若有系统外合（净）力为零，则系统内各质点相互作用力亦为零（可视为牛顿第三定律，作用力反作用力原理），故动量变化为零，所以动量守恒。

动量守恒定律具有普遍意义，适用于宏观、微观。

1.3 算例

因为动量是矢量，所以子弹从起先静止的枪中射出后，尽管子弹和枪都在运动，但由于子弹的动量与枪的动量等值反向，它们相互抵消，使得子弹与枪形成的系统中动量的总和依然为零。

重达3 Kg的步枪以800 m/s的枪口速度发射重达0.025 Kg的子弹。步枪和子弹的总动量可表示为:

ML = (3 Kg) (0 m/s) + (0.025 Kg) (0 m/s)

     = (3 Kg) u_r (m/s) + (0.025 Kg) (800 m/s)

     = 0

因此枪身的后坐速度为：

u_r = – (0.025 Kg) (800 m/s) / (3 Kg)

    = -6.667 (m/s)

枪身后坐的动能可计算为：

E = 1/2 m u_r²

   = 1/2 (3 Kg) (-6.667)²

   = 66.67 (N·m或焦耳J)

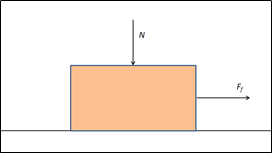
减慢后坐力所需的力取决于减慢距离。在减速距离s = 0.1m的情况下。

其后坐力可以计算为：

F = E / s

  = (66.67 N m) / (0.1 m)

  = 666.7 N 或 直观感受为：67.96 Kg

1 单摆定义

单摆是能够产生往复摆动的一种装置，将无重细杆或不可伸长的细柔绳一端悬于重力场内一定点，另一端固结一个重小球，就构成单摆。若小球只限于铅直平面内摆动，则为平面单摆，若小球摆动不限于铅直平面，则为球面单摆。

图 1

2 单摆周期

在小振幅（角α ≤ 5°）下，单摆做简谐运动的周期跟摆长的平方根成正比，跟重力加速度的平方根成反比，跟振幅、摆球的质量无关。

式 1

其中:

• T =一周期的振荡周期（s）
• L =摆的长度（m）
• g= 重力加速度（9.81 m/s²）

由于单摆的周期只与摆长l和重力加速度g相关，因此单摆可以作一个简单的计时器。

1  马力定义

马力（英语：horsepower，hp），俗称匹，是一个古老的功率单位。今日除了航空、造船与汽车工业提及内燃机的功率、空调的制冷性能以外，在其他领域较少用马力这个单位，而会使用标准的国际功率单位瓦特。 马力的定义有很多种，现今常用的两种马力为英制马力和公制马力，英制马力约为745.7W，公制马力约为735.5W。

马力单位概念是由蒸汽机改良者詹姆斯-瓦特命名，用以表示他的蒸汽机相对于马匹拉力的功率，定义为：一匹马在1分钟的时间，拖动半径为12英尺水车2.4圈，亦即(2.4*2π*12英尺)的距离*瓦特假设每匹马能拉动180磅，马力即可透过下式计算：功/时间=力*距离/时间=(180磅力)*(2.4*2π*12英尺)/1分钟=32572英尺·磅力/分钟。约等于33,000英尺‧磅力/分钟

有时为了区别不同的马力定义，会在马力符号hp的后面加上一个后缀，例如：hp(I)代表英制马力（Imperial horsepower）或机械马力，hp(M)代表公制马力（Metric horsepower），hp(S)代表蒸气马力（Steam horsepower），即锅炉马力，hp(E)代表电气马力（Electrical horsepower）。

液压马力与机械马力是相等的。以上公式乃是便于液压或水力系统中的计算。

2  空调匹数

空调系统的匹数不是指电功率。一匹是指制冷量8000-9000BTU/hr (2.34-2.64kW)的冷气机。功率1匹空调冷气机的电功率大约960W。

一匹的定频式冷气机（9000BTU/hr）的电功率一般介于800W到1000W。

一匹的变频式冷气机（1700-10,500BTU/hr）能够在250W到1250W间运行。若以供暖模式（12,000BTU/hr）运作，电功率可达到1600W。

注：BTU是英制热单位(British thermal unit，简称BTU，有时也被写成 Btu) 是一个传统英制的能量或热量单位，约等于 1055 焦耳，是将一磅的水由华氏39度加热至华氏40度所需的热能。 此一单位通常用在蒸汽机、暖气、冷气、电热等产业。

焦耳（J）是更为普遍的科学界通常使用 SI 制标准单位。

1 角运动中物体的力和力矩

旋转物体的功率可以表示为：

P = T·ω

   = T·2 π·n_rps  

   = T·π·n_rpm / 30    

式 1

其中：

• P = 功率 (W)
• T = 扭矩 (Nm)
• ω = 角速度 (rad/s)-弧度单位
• π = 3.14…
• n_rps = 每秒转数(rps, 1/s)
• n_rpm = 每分钟转数 (rpm, 1/min)

弧度-角度转换：1 rad = 360^o/ 2 π ≈ 57.29578^o

1.1 扭矩和扭力的关系

T = I·α 

式 2

• I = 转动惯量（kgˑm²）
• α=角加速度 (rad/s²)

2 算例

电动机以3600 rpm的速度旋转，测量的功率消耗为2000W。电动机产生的力矩（无损耗）可通过将式1重新排列计算得到：

T = 30 P / (π n_rpm) 

   = 30 (2000 W) / (π (3600 rpm))  

   = 5.3 Nm

 

 

1 纬度，高度对重力加速度的影响

重力加速度g的方向总是竖直向下的，但由于地球是非完美球体及其自转，重力加速度的方向并不通过地心。重力是万有引力的一个分力，万有引力的另一个分力提供了物

体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高，圆周运动轨道半径越小，需要的向心力也越小，重力将随之增大，重力加速度也变大。地理南北两极处的圆周运动轨道半径为0，需要的向心力也为0，重力等于万有引力，此时的重力加速度也达到最大。

1.1   各纬度的海平面高度的重力加速度（m/s²）

工科生小书架 | www.all4engieer.com为你梳理

纬度	重力加速度
0	9.7803
10	9.78186
20	9.78634
30	9.79321
40	9.80166
50	9.81066
60	9.81914
70	9.82606
80	9.83058
90	9.83218

表 1

1.2        不同高度的重力加速度 (m/s2）

工科生小书架 | www.all4engieer.com为你梳理

表 2

1.3        重力加速度g的几个常见取值

工科生小书架 | www.all4engieer.com为你梳理

地点	维度	重力加速度 (m/s2)
北极	90° 0′	9.8321
阿拉斯加（北美）	61° 10′	9.8218
格林威治	51° 29′	9.8119
巴黎	48° 50′	9.8094
北京	39° 56′	9.80122
巴拿马	8° 55′	9.7822
赤道	0° 0′	9.7799

表 3

1  牛顿第一定律

孤立质点保持静止或做匀速直线运动。

2 牛顿第二定律

物体加速度的大小跟作用力成正比，跟物体的质量成反比，且与物体质量的倒数成正比；加速度的方向跟作用力的方向相同。

3 牛顿第三定律

相互作用的两个质点之间的作用力和反作用力总是大小相等，方向相反，作用在同一条直线上。

4 自由落体的速度和距离

牛顿第二定律的重力表达式为：

W = F_g

    = m a_g        

    = m g 

其中：

• W，Fg =重量，重力（N）
• m =质量（kg）
• a_g = g =重力加速度（9.81 m / s²）

质量是物质一种属性-是标量，而力是向量。

可以通过测量与自由落体的时间变化相关的速度变化来观察重力加速度：

a_g = dv / dt

其中：

• dv =速度变化（m / s）
• dt =时间变化（秒）

自由落体在1秒内加速达到9.81 m / s的速度。

注意：忽略空气阻力时，靠近地面的重物和轻体将以相同的加速度掉落到地球上。

4.1 不同单位制下的重力加速度

1 a_g = 1 g = 9.81 m/s² = 35.30394 (km/h)/s

1 a_g = 1 g = 32.174 ft/s² = 386.1 in/s² = 22 mph/s

一段时间后自由落体的速度可以计算为：

v = a_g t  

其中：

• t =时间（s）
• v = 速度(m/s)

自由下落的物体经过一段时间后所经过的距离可以表示为：

s = 1/2 a_g t² 

其中：

• s =物体行进的距离（m）

4.2 自由落体的下落的速度和距离：

时间	速度	速度	速度	速度	距离	距离
(s)	m/s	km/h	ft/s	mph	m	ft
1	9.8	35.3	32.2	21.9	4.9	16.1
2	19.6	70.6	64.3	43.8	19.6	64.3
3	29.4	106	96.5	65.8	44.1	144.8
4	39.2	141	128.7	87.7	78.5	257.4
5	49.1	177	160.9	110	122.6	402.2
6	58.9	212	193	132	176.6	579.1
7	68.7	247	225.2	154	240.3	788.3
8	78.5	283	257.4	176	313.9	1,029.60
9	88.3	318	289.6	198	397.3	1,303.00
10	98.1	353	321.7	219	490.5	1608.7

表 1

注：上表为没有空气动力阻力（真空条件）的情况下实现了速度和距离。 真实情况取决于形状和表面积，较高速度的物体的空气阻力（或阻力）可能很大。

1  加速度方程

加速度：速度与所用时间的变化比率，可表示为：

2  算例

如果摩托车在3秒内从0 km / h加速到100 km / h，则加速度可以计算为：

a = ((100 km/h) – (0 km/h)) (1000 m/km) / (3600 s/h)) / (3 s)

    = 9.26 (m/s²)