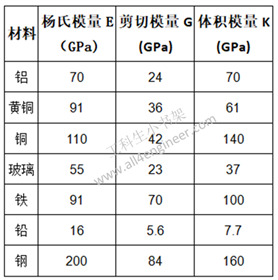
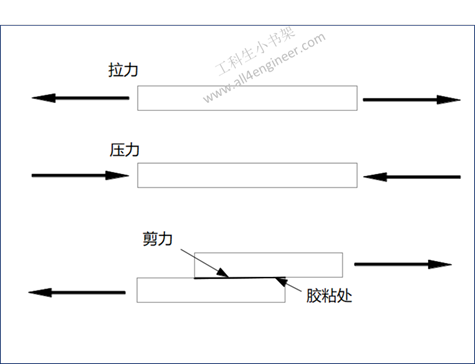
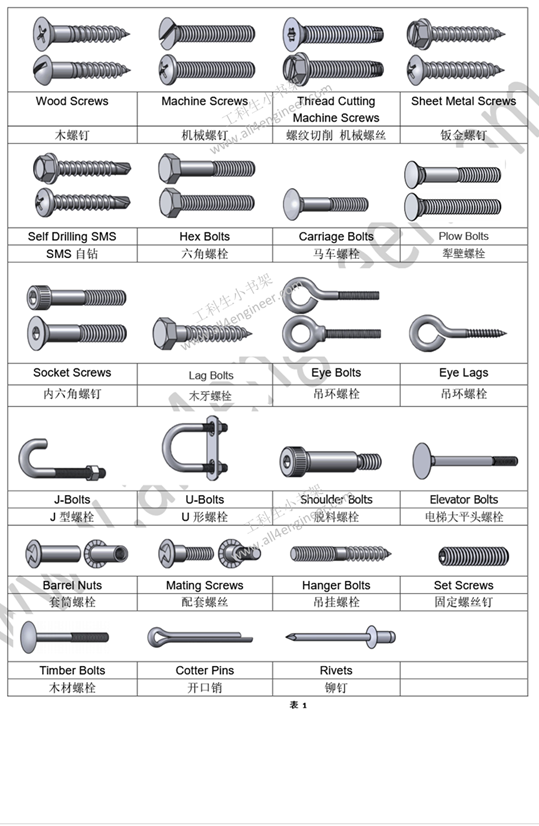
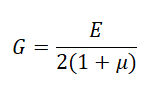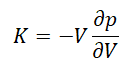1  划痕硬度

刻划硬度在矿物学里一般指物质刺入另外一种较软物质的能力。一个由硬物质构成的物体能在另一个由较软物质构成的物体上形成划痕。刻划硬度常以莫氏矿物硬度单位计算。

一种最常见的测量工具叫做莫氏硬度计。

莫氏硬度，是一种利用矿物的相对刻划硬度划分矿物硬度的标准，该标准是德国矿物学家腓特烈·摩斯（德语：Friedrich Mohs）于1812年提出的。

用测得的划痕的深度分十级来表示硬度：

滑石(talc)—— 1（硬度最小）

石膏(gypsum)—— 2

方解石(calcite)—— 3

萤石(fluorite)—— 4

磷灰石(apatite)—— 5

正长石(feldspar; orthoclase; periclase )—— 6

石英(quartz)—— 7

黄玉(topaz)—— 8

刚玉(corundum)——9

金刚石(diamond)—— 10。

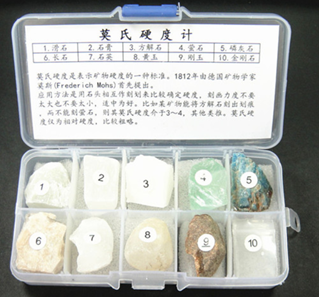
图 1

具体鉴定方法是，在未知硬度的矿物上选定一个平滑面，用上述已知矿物的一种加以刻划，如果未知矿物表面出现划痕，则说明未知矿物的硬度小于已知矿物；若已知矿物表面出现划痕，则说明未知矿物的硬度大于已知矿物。如此依次试验，即可得出未知矿物的相对硬度。若某种矿物的硬度在两种标准矿物之间，则会用.5表示，例如黄铁矿的莫氏硬度为6.5。

 

注：莫氏硬度仅为相对硬度，比较粗略。但莫氏硬度应用方便，可以随身携带，野外作业时常采用。

 

 

1 硬度 （Hardness）

硬度指固体材料抗拒永久形变的特性。材料局部抵抗硬物压入其表面的能力称为硬度。固体对外界物体入侵的局部抵抗能力，是比较各种材料软硬的指标。一般硬度越高，耐磨性越好。由于规定了不同的测试方法，所以有不同的硬度标准。

三种主要的硬度定义方式包括：

• 刻划硬度（Scratch hardness）
• 压入硬度（Indentation hardness）
• 回弹硬度（Rebound hardness，动态硬度dynamic hardness，或绝对硬度）

注意：各种硬度标准的力学含义不同，相互不能直接换算，但可通过试验加以对比。

2 硬度换算表

抗拉强度 N/mm2	维氏硬度 HV	布氏硬度 HB	洛氏硬度 HRC
255	80	76	–
270	85	80.7	–
285	90	85.2	–
305	95	90.2	–
320	100	95	–
335	105	99.8	–
350	110	105	–
370	115	109	–
380	120	114	–
400	125	119	–
415	130	124	–
430	135	128	–
450	140	133	–
465	145	138	–
480	150	143	–
490	155	147	–
510	160	152	–
530	165	156	–
545	170	162	–
560	175	166	–
575	180	171	–
595	185	176	–
610	190	181	–
625	195	185	–
640	200	190	–
660	205	195	–
675	210	199	–
690	215	204	–
705	220	209	–
720	225	214	–
740	230	219	–
755	235	223	–
770	240	228	20.3
785	245	233	21.3
800	250	238	22.2
820	255	242	23.1
835	260	247	24
850	265	252	24.8
865	270	257	25.6
880	275	261	26.4
900	280	266	27.1
915	285	271	27.8
930	290	276	28.5
950	295	280	29.2
965	300	285	29.8
995	310	295	31
1030	320	304	32.2
1060	330	314	33.3
1095	340	323	34.4
1125	350	333	35.5
1115	360	342	36.6
1190	370	352	37.7
1220	380	361	38.8
1255	390	371	39.8
1290	400	380	40.8
1320	410	390	41.8
1350	420	399	42.7
1385	430	409	43.6
1420	440	418	44.5
1455	450	428	45.3
1485	460	437	46.1
1520	470	447	46.9
1555	480	(456)	47.7
1595	490	(466)	48.4
1630	500	(475)	49.1
1665	510	(485)	49.8
1700	520	(494)	50.5
1740	530	(504)	51.1
1775	540	(513)	51.7
1810	550	(523)	52.3
1845	560	(532)	53
1880	570	(542)	53.6
1920	580	(551)	54.1
1955	590	(561)	54.7
1995	600	(570)	55.2
2030	610	(580)	55.7
2070	620	(589)	56.3
2105	630	(599)	56.8
2145	640	(608)	57.3
2180	650	(618)	57.8
	660		58.3
	670		58.8
	680		59.2
	690		59.7
	700		60.1
	720		61
	740		61.8
	760		62.5
	780		63.3
	800		64
	820		64.7
	840		65.3
	860		65.9
	880		66.4
	900		67
	920		67.5
	940		68

表 1

1        弹性模量

1.1        杨氏模量-拉压模量

杨氏模量也称杨氏模数（英语：Young’s modulus），一般将杨氏模量习惯称为弹性模量。弹性材料承受正向应力时会产生正向应变，在形变量没有超过对应材料的一定弹性限度时（符合胡克定律阶段），定义正向应力与正向应变的比值为这种材料的杨氏模量。其公式为：

E = 应力 / 应变

= σ / ε

= (F / A) / (dl / l₀)

式 1

其中：

• E = 杨氏模量 (Pa, N/m²)
• σ = 应力（N）
• ε =应变（m / m）
• F = 载荷（N）
• dl =物体的伸长或压缩量（m）
• l₀=物体原始的长度（m）

1.2        剪切模量

剪力模数（shear modulus）定义为剪应力与剪应变的比值

G = stress / strain

   = τ / γ

   = (F_p / A) / (s / d)

式 2

其中：

• G =剪切弹性模量-或刚性模量（N / m²）
• τ=剪应力（Pa，N / m²）
• γ=剪切应变表示符号
• F_p =平行于其作用面的力
• A =面积（m2）
• s =面的位移（m）
• d =位移面之间的距离（m）

1.3        杨氏模量和剪切模量的关系

在均质且等向性的材料中：

式 3

其中：     

• E=杨氏模量 (Young’s modulus )
• µ=泊松比 (Poisson’s ratio)
  

1.4        体积模量 （Bulk Modulus)

体积模量 （Bulk Modulus）也称为不可压缩量，是材料对于表面四周压强产生形变程度的度量。它被定义为产生单位相对体积收缩所需的压强。单位为：Pa（N/m²）

其计算公式为：

式 4

其中:

• p=压力 (N)
• V =体积 (m³)
•  ∂p/∂V=压力对体积的偏导数。

体积模量的倒数即为一种物质的压缩率。

2        常用材料的弹性模量

注：1 GPa = 109 Pa (N/m2)

1 应力

在连续介质力学里，应力定义为单位面积所承受的作用力。分类如下：

• 拉应力——趋于拉伸或拉长材料的应力-垂直于应力区域作用；
• 压应力——趋于压缩或缩短材料的应力-垂直于应力区域作用；
• 剪切应力——易于剪切材料的应力-在平面上以直角作用于受力区域，产生压缩应力或拉伸应力

图 1

1.1        拉应力或压应力

以上图为例，拉应力和压应力计算公式：

σ = F/A_截面

式 1

其中：

• σ =应力（Pa（N / m²））
• F =垂直于面积（N）的法向力
• A_截面 =截面面积（m²）

1.1.1   算例

10kN的拉力作用在圆形棒直径10mm的杆件上。杆中的应力可以计算为

σ = (10×10³N) / (π ((10×10^-3 m) / 2)²)

=127388535 (N/m²) 

=127 (MPa)

1.2 剪应力

以图1为例，剪应力计算公式：

σ = F/A_胶接面

式 2

其中：

• σ =应力（Pa（N / m²））
• F =平行于胶接处（N）的力
• A_胶接面 =胶接面面积（m²）

剪切力致使物体的两个部分趋于相互滑动的力。

2 应变（变形）

应变的定义：一微小材料元素承受应力时所产生的变形强度(或简称为单位长度变形量)，因此是一个无量纲量。

• 法向应变（正应变）-由法向力引起的应变；
• 剪切应变-由剪切力引起的应变。

法向应变，可以表示为

ε = dl / l_o

= σ / E

式 3

其中：

• dl = 长度变化量(m)
• l_o = 初始长度(m)
• ε = 应变（无单位）
• E = 杨氏模量 (Pa , N/m²)

2.1 算例

在已知杆件材料杨氏模量E=200 GPa，施加的应力为σ=127 MPa，杆件初始长度l₀=2m，计算杆件的伸长量：

dl = σ lo / E

= (127×10⁶ Pa) (2 m) / (200×10⁹ Pa) 

= 0.00127 m

= 1.27 mm

1 杨氏模量 E

杨氏模量也称杨氏模数（英语：Young’s modulus），一般将杨氏模量习惯称为弹性模量。弹性材料承受正向应力时会产生正向应变，在形变量没有超过对应材料的一定弹性限度时，定义正向应力与正向应变的比值为这种材料的杨氏模量。其公式为：

E = 应力 / 应变

= σ / ε

= (F / A) / (dL / L)

式 1

其中：

• E = 杨氏模量 (Pa, N/m²)
• σ = 应力（N）
• ε =应变（m / m）
• F = 载荷（N）
• dL =物体的伸长或压缩量（m）
• L =物体原始的长度（m）

2 应变-ε

应变是“由于应力导致的固体变形”-尺寸变化除以尺寸的原始值-可以表示为

ε = dL / L

式 2

其中：

• ε =应变（m / m）
• dL =物体（m）的伸长或压缩
• L =物体的长度（m）

只要应力小于材料的屈服强度，就可以用上式来预测物体的伸长或压缩量。

3 应力-σ

应力是每单位面积所受的力，可以表示为：

σ= F / A

式 3

其中：

• σ=应力（N / m²）
• F =施加力（N，lb）
• A =物体的受力面积（m²）

4  常见材料拉伸杨氏模量，抗拉强度和屈服强度。

材料	拉伸模量 E（GPa）	极限抗拉强度 σ（MPa）	屈服强度 σ（MPa）
ABS塑料	1.4-3.1	40	–
亚克力(丙烯酸塑料)	3.2	70	–
铝青铜	120	–	–
铝	69	110	95
铝合金	70	–	–
锑	78	–	–
芳纶	70-112	–	–
铍	287	–	–
铍铜	124	–	–
铋	32	–	–
硼	–	–	3100
黄铜	102-125	250	–
海军黄铜	100	–	–
青铜	96-120	–	–
镉	32	–	–
碳纤维增强塑料	150	–	–
碳纳米管，单壁	1000	–	–
铸铁4.5％C，ASTM A-48	–	170	–
纤维素，棉花，木浆和再生	–	80-240	–
醋酸纤维素，模制	–	Dec-58	–
醋酸纤维素片	–	30-52	–
硝酸纤维素，赛璐oid	–	50	–
氯化聚醚	1.1	39	–
氯化PVC（CPVC）	2.9	–	–
铬	248	–	–
钴	207	–	–
水泥	17	–	–
铜	117	220	70
钻石（C）	1220	–	–
环氧树脂	3	26-85	–
纤维板，中密度	4	–	–
亚麻纤维	58	–	–
玻璃	50-90	50	–
玻璃纤维增​​强聚酯基体	17	–	–
金	74	–	–
花岗岩	52	–	–
石墨烯	1000	–	–
灰铸铁	130	–	–
麻纤维	35	–	–
因科内尔	214	–	–
铱	517	–	–
铁	210	–	–
铅	13.8	–	–
金属镁（Mg）	45	–	–
锰	159	–	–
大理石	–	15	–
MDF-中密度纤维板	4	–	–
汞	–	–	–
钼（Mo）	329	–	–
蒙乃尔金属	179	–	–
镍	170	–	–
镍银	128	–	–
镍钢	200	–	–
铌（Co）	103	–	–
尼龙6	2-Apr	45-90	45
尼龙66	–	60-80	–
橡木（沿纹理）	11	–	–
酚醛树脂	–	33-59	–
苯酚甲醛模塑料	–	45-52	–
磷青铜	116	–	–
松木（沿纹理）	9	40	–
铂	147	–	–
钚	97	–	–
聚丙烯腈，纤维	–	200	–
聚苯并恶唑	3.5	–	–
聚碳酸酯	2.6	52-62	–
聚乙烯HDPE（高密度）	0.8	15	–
聚对苯二甲酸乙二醇酯，PET	2-2.7	55	–
聚酰胺纤维	2.5	85	–
聚异戊二烯，硬橡胶	–	39	–
聚甲基丙烯酸甲酯（PMMA）	2.4-3.4	–	–
聚酰亚胺芳烃	3.1	68	–
聚丙烯，PP	1.5-2	28-36	–
聚苯乙烯，PS	3-3.5	30-100	–
聚乙烯，LDPE（低密度）	0.11-0.45	–	–
聚四氟乙烯（PTFE）	0.4	–	–
聚氨酯浇铸液	–	Oct-20	–
聚氨酯弹性体	–	29-55	–
聚氯乙烯（PVC）	2.4-4.1	–	–
钾盐	–	–	–
铑	290	–	–
橡胶，小应变	0.01-0.1	–	–
蓝宝石	435	–	–
硒	58	–	–
硅	130-185	–	–
碳化硅	450	–	3440
银	72	–	–
钠	–	–	–
钢，高强度合金ASTM A-514	–	760	690
精钢AISI 302	180	860	502
钢，结构ASTM-A36	200	400	250
钽	186	–	–
钍	59	–	–
锡	47	–	–
钛	–	–	–
钛合金	105-120	900	730
牙釉质	83	–	–
钨（W）	400-410	–	–
碳化钨（WC）	450-650	–	–
铀	170	–	–
钒	131	–	–
铁艺	190-210	–	–
锌锌	83	–	–

表 1

1 Pa (N/m²) = 1×10^-6 N/mm² = 1.4504×10^-4 psi

1 MPa = 10⁶ Pa (N/m²) = 0.145×10³ psi (lb_f/in²) = 0.145 ksi

1 GPa = 10⁹ N/m² = 10⁶ N/cm²  = 10³ N/mm² = 0.145×10⁶ psi (lb_f/in²)

1 Mpsi = 10⁶ psi = 10³ ksi

1 psi (lb/in²) = 0.001 ksi = 144 psf (lb_f/ft²) = 6,894.8 Pa (N/m²) = 6.895×10^-3 N/mm²

1  紧固件类别

紧固件类型参考文献下载：fastener-types.pdf

1 泊松比

泊松比是指材料在单向受拉或受压时，横向正应变与轴向正应变的绝对值的比值，也叫横向变形系数，它是反映材料横向变形的弹性常数。

图 1

在材料的弹性范围内加载，泊松比计算为：

µ= |-∆W/W| / |∆L/L|

2 常见金属的泊松比：

金属名称	– μ –
铝	0.33
铝青铜	0.3
铍	0.024 – 0.03
铸铁	0.26
青铜	0.34
铜	0.36
金	0.42
铅	0.40 – 0.45
镁	0.35
软钢	0.3
钼	0.32
黄铜	0.34
镍	0.31
磷青铜	0.33
铂	0.39
钚	0.15 – 0.21
银	0.37
不锈钢	0.3
钽	0.35
钍	0.27
锡	0.33
钛	0.3
钨丝	0.28
铀	0.21
铁	0.3
锌	0.25

1 重心和浮心的定义

重心是指地球对物体中每一微小部分引力的合力作用点。体积，面积或线的“重心”是物体（如果悬吊起来）将达到平衡的点。

浮心是指浮体或潜体水下部分体积的形心。当浮体方位在铅直面内发生偏转时，其水下部分的体积虽保持不变，但其形状却发生变化，因而浮心的位置也相应地移动。

浮心和重心的相对位置对于判断浮体是否为稳定平衡有重要意义。

图 1

当船体垂直时，重心和浮力中心在同一垂直线上，船体是稳定态。

对于大多数船体，浮力中心低于重心，并且船体被认为是亚稳定态。

当船体倾斜时，重心保持在与船体相关的相同位置（只要船体没有变化和/或货物没有移动）。 浮力中心将移动以适应新的重心，以适应船体的排水量。

在开始时，重力和浮力将产生一个附加扭矩将船体移回垂直位置。

但如果船体倾斜太多，则浮力中心将移至浮力和重力开始产生作用于相同方向的力矩的位置，那么船体将

倾覆。

质量中心简称质心，指物质系统上被认为质量集中于此的一个假想点。

1        质心计算公式

式 1

其中：

• m 为系统内单个质点的质量
• r 为各质点相对于某一坐标原点的距离
• M 为系统的总质量

若选择不同的坐标系，质心坐标的具体数值就会不同，质心相对于质点系中各质点的相对位置与坐标系的选择无关。质点系的质心仅与各质点的质量大小和分布的相对位置有关

2        算例

图 1

质心位置计算：

取m_a处为坐标原点

R_x = (m_a r_a + m_b r_b) / (m_a + m_b)

= (m_b / (m_a + m_b)) d 

式 2

其中：

• R_x=重心的x坐标

重心是指地球对物体中每一微小部分引力的合力作用点。体积，面积或线的“重心”是物体（如果悬吊起来）将达到平衡的点。

1 基于周长的重心计算

图 1

重心是三角形ABC（三角形边的中点）上刻有圆的中心。

距离d的计算：

d = h（b + c）/ 2（a + b + c）

式 1

2 三角形重心的计算

图 2

三角形的重心在直线BE和AD的交点处。

距离a的计算：

a = h / 3 

式 2

3 平行四边形的重心的计算

图 3

平行四边形的重心在对角线的交点处。

4 梯形的重心的计算

图 4

梯形的重心可以通过将梯形分成两个三角形来估算。重心将在中线CD和三角形重心之间的线的交点处。

5 两个物体的重心的计算

图 5

两个物体的重心用以下公式计算：

b = Q a / (P + Q)

c = P a / (P + Q)

其中：

• P, Q为物体的重量或者质量（N，Kg）

常见工程材料如钢，塑料，陶瓷和复合材料的典型属性

1 复合材料

材料	密度- ρ – (103 kg/m3)	拉伸模量- E – (GPa)	抗拉强度- σ – (MPa)	比模量- E / ρ –	比强度- σ / ρ –	最高使用温度(oC)
玻璃-环氧树脂（35％）	1.9	25	300	13.2	0.16	80 – 200
玻璃纤维-聚酯（35％）	2	15.7	130	7.85	0.065	80 – 125
玻璃纤维尼龙（35％）	1.6	14.5	200	8.95	0.12	75 – 110
高强度玻璃纤维-环氧树脂（45％）	1.8	39.5	870	21.8	0.48	80 – 215
环氧碳（61％）	1.6	142	1730	89.3	1.08	80 – 215
芳纶环氧（53％）	1.35	63.6	1100	47.1	0.81	80 – 215

表 1

2        金属

材料	密度- ρ – (103 kg/m3)	拉伸模量- E – (GPa)	抗拉强度- σ – (MPa)	比模量- E / ρ –	比强度- σ / ρ –	最高使用温度(oC)
铸铁	7.15	100	140	14.3	0.02	230 – 300
钢，AISI 1045	7.7 – 8.03	205	585	26.3	0.073	500 – 650
铝-2045-T4	2.7	73	450	27	0.17	150 – 250
铝-6061-T6	2.7	69	270	25.5	0.1	150 – 250

表 2

3        陶瓷

材料	密度- ρ – (103 kg/m3)	拉伸模量- E – (GPa)	抗拉强度- σ – (MPa)	比模量- E / ρ –	比强度- σ / ρ –	最高使用温度(oC)
氧化铝	3.8	350	170	92.1	0.045	1425-1540
氧化镁	3.6	205	60	56.9	0.017	900-1000

表 3

4        塑料

材料	密度- ρ – (103 kg/m3)	拉伸模量- E – (GPa)	抗拉强度- σ – (MPa)	比模量- E / ρ –	比强度- σ / ρ –	最高使用温度(oC)
尼龙	1.15	2-3.6	82	2.52	0.071	75-100
聚乙烯（HDPE）	0.9-1.4	0.18-1.6	15
聚丙烯	0.9-1.24	1.4	33	1.55	0.037	50-80
环氧树脂	1.25	3.5	69	2.8	0.055	80-215
酚醛	1.35	3	6	2.22	0.004	70-120

注：

1 GPa = 1x10⁹ Pa = 1.45x10⁵psi

1 MPa = 10⁶ Pa

1 kg/m³ = 0.0624 lb/ft³

1 惯性矩计算

面惯性矩或面积惯性矩-也称为面积第二矩- I，是一种形状特性，用于预测梁的挠度，弯曲和应力等。

绕轴弯曲的惯性矩的一般公式可以表示为

I_x = ∫ y² dA 

其中：

• I_x=与轴相关的惯性面积矩（m⁴，mm⁴，in⁴，ft⁴）
• y =轴到元素dA的垂直距离（m，mm，in，ft）
• dA=元素面积（m²，mm²，in²，ft²）

2 常见截面惯性矩

2.1 矩形

2.2 圆形

2.3  圆环

2.4  工字钢

3 惯性矩单位转换器

单位	m4	cm4	mm4
m4	1	108	1012
cm4	10-8	1	104
mm4	10-12	10-4	1

1        悬臂梁的单点载荷计算

图 1

1.1        弯矩计算

M_A = – F a b (L + b) / (2 L²)

式 1

其中：

M_A =固定端A的力矩（Nm）

F = 载荷 (N)

M_F = R_b b

其中：

• M_F =负载点F的力矩（Nm）
• R_b =支撑B处的支反力（N）

1.2        挠度计算

δ_F = F a³ b² (3 L + b) / (12 L³ E I)  

式 2

其中：

• δmax=挠度（m）
• E =弹性模量（Pa（N / m²），N / mm²，psi）
• I =惯性面积矩（m⁴，mm⁴）

1.3        支反力计算

R_A = F b (3 L² – b²) / (2 L³)

式 3

R_A =固定端A的支反力（N）

R_B = F a² (b + 2 L ) / (2 L³) 

式 4

• R_B =固定端B的支反力（N）

2 悬臂梁的均布载荷计算

图 2

2.1 弯矩计算

M_A = – q L² / 8 

式 5

其中：

• M_A =固定端A的力矩（Nm）
• q = 均布载荷 (N/m)

M₁ = 9 q L² / 128

式 6

其中：

• M₁ = 0.625 L（Nm）时为最大弯矩

2.2 挠度计算

δ_max = q L⁴ / (185 E I)

式 7

其中：

• δmax= 0.579 L（Nm）时为最大挠度

δ_1/2 = q L⁴ / (192 E I)  

式 8

• δ_1/2 = L / 2   (m) 的挠度

2.3 支反力计算

R_A = 5 q L / 8

式 9

• R_A =固定端A的支反力（N）

R_B = 3 q L / 8 

式 10

• R_B =固定端B的支反力（N）

3 悬臂梁的梯形载荷计算

图 3

3.1        弯矩计算

M_A = – q L² / 15 

式 11

其中：

• M_A =固定端A的力矩（Nm）
• q = 梯形载荷 (N/m)

M₁ = q L² / 33.6

式 12

其中：

• M₁ = 0.553 L（Nm）时为最大弯矩

3.2 挠度计算

δ_max = q L⁴ / (419 E I)

式 13

其中：

• δmax= 0.553 L（Nm）时为最大挠度

δ_1/2 = q L⁴ / (427 E I)  

式 14

• δ_1/2 = L / 2   (m) 的挠度

3.3 支反力计算

R_A = 2 q L / 5 

式 15

• R_A =固定端A的支反力（N）

R_B = q L / 10

式 16

• R_B =固定端B的支反力（N）

4 悬臂梁的附加弯矩计算

图 4

4.1 弯矩计算

M_A = -M_B / 2

式 17

其中：

• M_A =固定端A的力矩（Nm）

4.2 挠度计算

δ_max = M_B L² / (27 E I) 

式 18

其中：

• δ_max = 2/3 L  (m)为最大挠度

4.3 支反力计算

R_A = 3 M_B / (2 L)

式 19

• R_A =固定端A的支反力（N）

R_B = – 3 M_B / (2 L) 

式 20

• R_B =固定端B的支反力（N）

1 简支梁单点载荷计算

图 1

1.1 弯矩计算

MA = – F a b² / L2  

式 1

其中：

• MA =固定端A处的力矩（Nm）
• F = 载荷 (N)

MB = – F a² b / L² 

式 2

• M_B =固定端B的力矩（Nm）

M_F = 2 F a² b² / L³ 

式 3

• M_F =点载荷时的力矩（Nm）

1.2 挠度计算

δ_F = F a³ b³ / (3 L³ E I) 

式 4

• δ_F=点载荷时的挠度（m）
• E =弹性模量（Pa（N / m²），N / mm²）
• I =惯性面积矩（m⁴，mm⁴）

1.3 支反力计算

R_A = F (3 a + b) b² / L³

式 5

• R_A =固定端A的支反力（N）

R_B = F (a + 3 b) a² / L³  

式 6

• R_B =固定端B的支反力（N）

2 简支梁的均布载荷计算

图 2

2.1        弯矩计算

M_A = – q L² / 20  

式 7

• M_A =固定端A的力矩（Nm）
• q =均匀下降载荷（N / m）

M_B = – q L² / 30  

式 8

• M_B =固定端B的力矩（Nm）

M₁ = q L² / 46.6  

式 9

• M₁ = 0.475 L（Nm）时的力矩

2.2 挠度计算

δ_max = q L⁴ / (384 E I)

式 10

• δ_max=中心的最大挠度（m）
• E =弹性模量（Pa（N / m²），N / mm²，psi）
• I =惯性面积矩（m⁴，mm⁴）

2.3 支反力计算

R_A = R_B

    = q L / 2 

式 11

• R =固定端的支反力（N）

3        简支梁梯形分布载荷计算

图 3

3.1 弯矩计算

M_A = – q L² / 20  

式 12

• M_A =固定端A的力矩（Nm）
• q =均匀下降载荷（N / m ）

M_B = – q L² / 30 

式 13

• M_B =固定端B的力矩（Nm）

M₁ = q L² / 46.6

式 14

• M₁ = 0.475 L（Nm）时的力矩

3.2 挠度计算

δ_max = q L⁴ / (764 E I) 

式 15

• δ_max= 0.475 L（m）时的最大挠度
• E =弹性模量（Pa（N / m²），N / mm²，psi）
• I =惯性面积矩（m⁴，mm⁴）

δ_1/2 = q L⁴ / (768 E I) 

式 16

• δ_1/2 = 0.5 L 时的挠度(m)

3.3 支反力计算

R_A = 7 q L / 20

式 17

• R_A =固定端A的支反力（N）

R_B = 3 q L / 20

式 18

• R_B =固定端B的支反力（N）

4 简支梁部分均匀的连续分布载荷计算

图 4

4.1        弯矩计算

M_A = – (q a² / 6) (3 – 4 a / l + 1.5 (a / L)²)

式 19

其中：

• M_A =固定端A的力矩（Nm）
• q =部分均匀载荷（N / m ）

M_B = – (q a² / 3) (a / L – 0.75 (a / L)²)

式 20

• M_B =固定端B的力矩（Nm）

4.2        支反力计算

R_A = q a (L – 0.5 a) / L – (M_A – M_B) / L 

式 21

其中：

• R_A =固定端A的支反力（N）

R_B = q a² / (2 L) + (M_A – M_B) / L    

式 22

• R_B =固定端B的支反力（N）