1 PP(聚丙烯)
1.1 什么是PP?
聚丙烯(Polypropylene)是一种由丙烯单体生产的坚韧,刚性和结晶的热塑性塑料。 它是线性烃树脂。 聚丙烯的化学式为 (C3H6)n。
聚丙烯于1951年由两位名叫Paul Hogan和Robert Banks的菲利普斯石油科学家首先聚合,后来由意大利和德国科学家Natta和Rehn聚合。 在意大利化学家朱利奥·纳塔(Giulio Natta)教授首次将其聚合后不到三年的时间里,随着商业化生产的开始,这种方法就变得极为突出。 Natta于1954年在西班牙完善并合成了第一种聚丙烯树脂,聚丙烯的结晶能力引起了极大的兴趣。 到1957年,它的知名度激增,整个欧洲开始了广泛的商业生产。 如今,它已成为世界上最常用的塑料之一。PP也是当今最便宜的塑料之一。
聚丙烯通常被称为塑料工业的“钢”,因为可以通过多种方式对其进行改性或定制,以最佳地满足特定目的。通常可以通过向其中引入特殊的添加剂或以非常特殊的方式制造来实现。
1.2 如何生产PP?
聚丙烯是由丙烯单体(一种不饱和有机化合物-化学式C3H6)的聚合反应通过以下方法制得的:
- 齐格勒-纳塔聚合方法
- 茂金属催化聚合方法
聚合后,PP可以根据甲基的位置形成三个基本链结构:
无规(Atactic PP)-不规则甲基(CH3)排列
等规(Isotactic PP)–甲基(CH3)排列在碳链的一侧
间规(Syndiotactic PP)-交替甲基(CH3)排列

图 1
1.3 PP的类型
聚丙烯的两种主要类型是均聚物和共聚物:
- 聚丙烯均聚物是使用最广泛的通用级产品。它仅包含半结晶固体形式的丙烯单体。
- 聚丙烯共聚物家族进一步分为无规共聚物和通过丙烯和乙烷聚合制得的嵌段共聚物:
- 聚丙烯无规共聚物是通过将乙烯和丙烯聚合在一起制成的。它具有乙烯单元,通常含量不超过6%(质量),随机掺入聚丙烯链中。这些聚合物具有柔韧性和光学透明性,使其适合需要透明性的应用以及需要出色外观的产品。
- 聚丙烯嵌段共聚物中,乙烯含量较大(5%至15%)。它具有以规则图案(或嵌段)排列的共聚单体单元。因此,规则图案使热塑性塑料比无规共聚物更坚韧,更不易碎。这些聚合物适用于要求高强度的应用,例如工业用途。
1.4 PP的特点
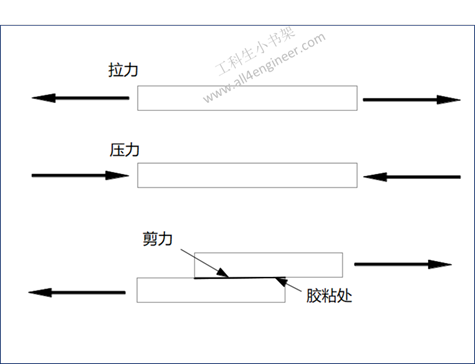
聚丙烯具有相对光滑的表面,可以使其在齿轮等低摩擦应用中或用作家具的接触点时,可以替代乙缩醛(POM)等塑料。这种品质的负面影响是,可能难以将聚丙烯粘合到其他表面(即它不能很好地粘合到某些与其他塑料配合得很好的胶水上,有时在需要形成接头的情况下必须焊接) )。尽管聚丙烯在分子水平上很滑,但它确实具有相对较高的摩擦系数,这就是为什么要使用缩醛,尼龙或PTFE代替的原因。聚丙烯相对于其他普通塑料还具有低密度,这对于注塑聚丙烯零件的制造商和分销商而言可减轻重量。它在室温下对脂肪等有机溶剂具有出色的抵抗力,但在高温下会发生氧化(注塑过程中的潜在问题)。
聚丙烯的主要优点之一是,可以将其制造(通过CNC或注塑,热成型或压接)成活动铰链。活动铰链是非常薄的塑料片,可以弯曲而不会破裂(即使在接近360度的极端运动范围内)。它们对于诸如举起沉重的门之类的结构应用不是特别有用,但对于诸如番茄酱或洗发水瓶子上的盖子之类的非承重应用则特别有用。聚丙烯是活动铰链的独特代表,因为它在反复弯曲时不会断裂。另一个优势之一是,聚丙烯可以进行CNC加工,包括活动铰链,从而可以更快地开发原型,并且比其他原型制作方法便宜。创新机制的独特之处在于我们能够用单片聚丙烯加工活动铰链。
聚丙烯的另一个优点是,它可以很容易地与其他聚合物(例如聚乙烯)共聚(基本上可以组合成复合塑料)。共聚显著改变了材料的性能,与纯聚丙烯(更多的是自己的商品塑料)相比,可实现更坚固的工程应用。
在商品塑料中密度最低。
1.5 PP 的优点
- 耐化学性:稀释的碱和酸不会轻易与聚丙烯反应,这使其成为此类液体容器(例如清洁剂,急救产品等)的理想选择。
- 弹性和韧性:聚丙烯会在一定的挠度范围内发挥弹性(就像所有材料一样),但在变形过程的早期也会经历塑性变形,因此通常被认为是“韧性”材料。韧性是一个工程术语,定义为材料变形(塑性,而非弹性)而不破裂的能力。
- 耐疲劳性:聚丙烯在经过大量的扭曲,弯曲和/或弯曲后仍保持其形状。此属性对于制作活动铰链特别有价值。
- 绝缘:聚丙烯具有很高的抗电性,对于电子元件非常有用。
- 透射率:尽管可以使聚丙烯透明,但通常将其制成自然不透明的颜色。聚丙烯可用于某些重要的光传输或具有美感的应用。如果需要高透射率,则最好选择丙烯酸或聚碳酸酯之类的塑料。
1.6 PP 的缺点
- 聚丙烯具有高的热膨胀系数,这限制了其高温应用。
- 聚丙烯易受紫外线降解的影响。
- 聚丙烯对氯化溶剂和芳烃的抵抗力较差。
- 已知聚丙烯很难喷涂,因为它的粘合性能很差。
- 聚丙烯是高度易燃的。
- 聚丙烯易于氧化。
- (尽管有缺点,但聚丙烯总体上还是一种很好的材料。 它具有其他材料所没有的独特品质,这使其成为许多项目的理想选择。)
1.7 应用举例
包装,纺织品,医疗保健,管道,汽车和电气应用。洗碗机安全的盘子,托盘,杯子等,不透明的可移动容器以及许多玩具。
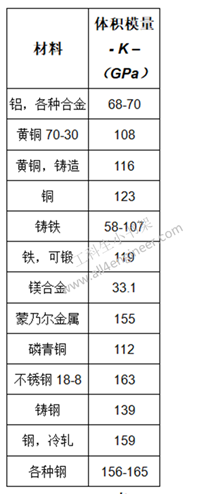
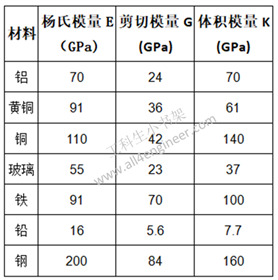
1.8 材料属性参数

表 1